Hai đường thẳng song song
Vị trí tương đối của hai đường thẳng trong không gian. Hai đường thẳng song song. Chứng minh đường thẳng song. Viết phương trình mặt phẳng chứa hai đường thẳng song song nhau.
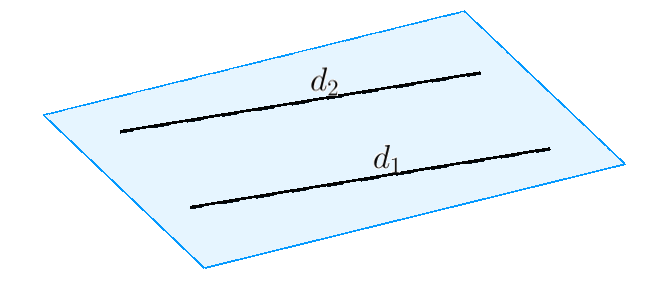
$d_1$ đi qua điểm $M_1$ và có vector chỉ phương ${\vec u_1}.$
$d_2$ đi qua điểm $M_2$ và có vector chỉ phương ${\vec u_2}.$
$d_2$ đi qua điểm $M_2$ và có vector chỉ phương ${\vec u_2}.$
$d_1$ song song $d_2$ $ \Leftrightarrow \left\{ \begin{array}{l}
{d_1} \cap {d_2} = \emptyset \\
{{\vec u}_1}\parallel {{\vec u}_2}.
\end{array} \right.$
Ví dụ. Chứng minh hai đường thẳng
$\left( {{d_1}} \right):\left\{ \begin{array}{l}
x + y + z - 5 = 0\,\,\,\,\left( * \right)\\
x - 3y + 6 = 0
\end{array} \right.$ và $\left( {{d_2}} \right):\left\{ \begin{array}{l}
x = 1 - 3t\\
y = - 1 - t\\
z = 1 + 4t
\end{array} \right.$ song song nhau.
Giải. Đầu tiên ta chứng minh $d_1$ không có giao điểm với $d_2$, khi đó có hay trường hợp xảy ra là chúng song song hoặc chéo nhau.
Thay $x = 1 + 3t,y = - 1 + t,z = 1 - 4t$ vào $\left( * \right)$ ta được $ - 4 = 0$. Vô lý.Suy ra ${d_1} \cap {d_2} = \emptyset .\,\,\,\,\,\,\left( \otimes \right)$.
Mặt khác từ phương trình tổng quát, ta được cặp vector pháp tuyến của $d_1$ là ${\vec n_1} = \left( {1;1;1} \right)$ và ${\vec n_2} = \left( {1; - 3;0} \right).$ Suy ra vector chỉ phương của $d_1$ là ${\vec u_{{d_1}}} = \left[ {{{\vec n}_1},{{\vec n}_2}} \right] = \left( {3,1, - 4} \right)$. Vector này cùng phương với ${\vec u_{{d_2}}} = \left( { - 3; - 1;4} \right).$ $\left( { \otimes \otimes } \right)$
Từ $\left( \otimes \right)$ và $\left( { \otimes \otimes } \right)$ suy ra $d_1$ song song với $d_2$.
Thay $x = 1 + 3t,y = - 1 + t,z = 1 - 4t$ vào $\left( * \right)$ ta được $ - 4 = 0$. Vô lý.Suy ra ${d_1} \cap {d_2} = \emptyset .\,\,\,\,\,\,\left( \otimes \right)$.
Mặt khác từ phương trình tổng quát, ta được cặp vector pháp tuyến của $d_1$ là ${\vec n_1} = \left( {1;1;1} \right)$ và ${\vec n_2} = \left( {1; - 3;0} \right).$ Suy ra vector chỉ phương của $d_1$ là ${\vec u_{{d_1}}} = \left[ {{{\vec n}_1},{{\vec n}_2}} \right] = \left( {3,1, - 4} \right)$. Vector này cùng phương với ${\vec u_{{d_2}}} = \left( { - 3; - 1;4} \right).$ $\left( { \otimes \otimes } \right)$
Từ $\left( \otimes \right)$ và $\left( { \otimes \otimes } \right)$ suy ra $d_1$ song song với $d_2$.
Bài tập
Tác giả bài viết: Cùng Học Toán




Góp ý hoặc một bài toán của Quý học viên hoặc Quý Phụ Huynh