Hình chiếu vuông góc của đường thẳng lên mặt phẳng
Hình chiếu vuông góc của đường thẳng lên mặt phẳng trong không gian. Cách tìm hình chiếu của đường thẳng lên mặt phẳng trong không gian.
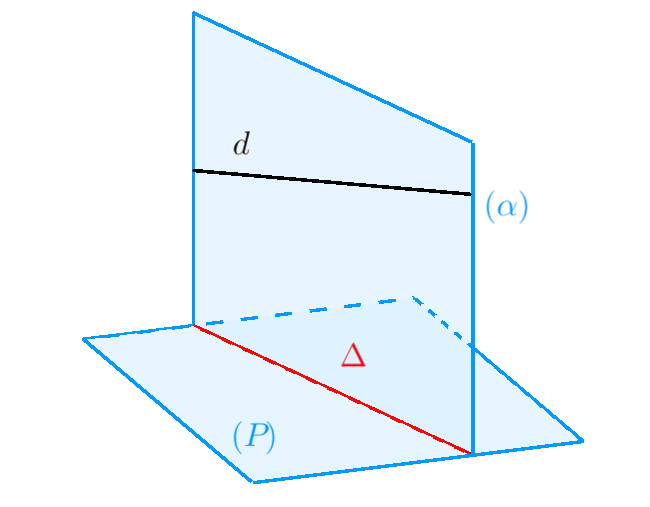
Bước 1. Viết phương trình mặt phẳng $\left( \alpha \right)$ chứa $d$ và vuông góc với $\left( P \right)$. Cặp vector chỉ phương của $\left( P \right)$ là ${\vec n_P}$ và ${\vec u_d}.$
Bước 2. Viết phương trình đường thẳng $\Delta = \left( \alpha \right) \cap \left( P \right).$
Ví dụ. Cho $\left( d \right):\left\{ \begin{array}{l}
x = 1 - t\\
y = 2 + 2t\\
z = - 1 - t
\end{array} \right.$ và $\left( P \right):x - y + z - 1 = 0.$
Viết phương trình tham số của đường thẳng $\Delta$ là hình chiếu vuông góc của $d$ lên $(P)$.
x = 1 - t\\
y = 2 + 2t\\
z = - 1 - t
\end{array} \right.$ và $\left( P \right):x - y + z - 1 = 0.$
Viết phương trình tham số của đường thẳng $\Delta$ là hình chiếu vuông góc của $d$ lên $(P)$.
Giải. Bước 1. Gọi $\left( \alpha \right)$ là mặt phẳng chứa $d$ và vuông góc với $\left( P \right)$. Cặp vector chỉ phương của $\left( \alpha \right)$ là ${\vec u_d} = \left( { - 1;2; - 1} \right),{\vec n_P} = \left( {1; - 1;1} \right)$. Suy ra ${\vec n_\alpha } = \left[ {{{\vec u}_d},{{\vec n}_P}} \right] = \left( {1;0 - 1} \right).$ Chọn $M\left( {1;2; - 1} \right) \in d \subset \left( \alpha \right).$
Phương trình của mặt phẳng $\left( \alpha \right)$ là $\left( {x - 1} \right) + 0\left( {y - 2} \right) - 1\left( {z + 1} \right) = 0 \Leftrightarrow x - z - 2 = 0.$
Bước 2. Hình chiếu vuông góc của $d$ lên mặt phẳng $\left( P \right)$ là $\Delta = \left( \alpha \right) \cap \left( P \right).$
Do đó phương trình tổng quát của $\Delta$ là $\left( \Delta \right):\left\{ \begin{array}{l}
x - y + z - 1 = 0\\
x - z - 2 = 0
\end{array} \right..$
Từ đây ta có cặp vector pháp tuyến của $\Delta$ là ${\vec n_1} = \left( {1, - 1;1} \right),{\vec n_2} = \left( {1,0; - 1} \right) \Rightarrow {\vec u_\Delta } = \left[ {{{\vec n}_1},{{\vec n}_2}} \right] = \left( {1;2;1} \right).$
Từ phương trình tổng quát của $\Delta$ ta thay $x = 0 \Rightarrow y = - 3,z = - 2 \Rightarrow A\left( {0; - 3; - 2} \right) \in \Delta .$
Suy ra phương trình tham số của $\Delta$ là $$\left( \Delta \right):\left\{ \begin{array}{l}
x = t\\
y = - 3 + 2t\\
z = - 2 + t
\end{array} \right..$$
Phương trình của mặt phẳng $\left( \alpha \right)$ là $\left( {x - 1} \right) + 0\left( {y - 2} \right) - 1\left( {z + 1} \right) = 0 \Leftrightarrow x - z - 2 = 0.$
Bước 2. Hình chiếu vuông góc của $d$ lên mặt phẳng $\left( P \right)$ là $\Delta = \left( \alpha \right) \cap \left( P \right).$
Do đó phương trình tổng quát của $\Delta$ là $\left( \Delta \right):\left\{ \begin{array}{l}
x - y + z - 1 = 0\\
x - z - 2 = 0
\end{array} \right..$
Từ đây ta có cặp vector pháp tuyến của $\Delta$ là ${\vec n_1} = \left( {1, - 1;1} \right),{\vec n_2} = \left( {1,0; - 1} \right) \Rightarrow {\vec u_\Delta } = \left[ {{{\vec n}_1},{{\vec n}_2}} \right] = \left( {1;2;1} \right).$
Từ phương trình tổng quát của $\Delta$ ta thay $x = 0 \Rightarrow y = - 3,z = - 2 \Rightarrow A\left( {0; - 3; - 2} \right) \in \Delta .$
Suy ra phương trình tham số của $\Delta$ là $$\left( \Delta \right):\left\{ \begin{array}{l}
x = t\\
y = - 3 + 2t\\
z = - 2 + t
\end{array} \right..$$
Bài tập
(nhiều bài tập hơn khi đăng ký học tại Trung tâm Cùng học toán)
Tác giả bài viết: Cùng Học Toán
Góp ý hoặc một bài toán của Quý học viên hoặc Quý Phụ Huynh




Chổ tìm điểm A thuộc đenta, sao lại thay x=0 ạ??
@Thảo Chào Thảo,
Ở đây mình cần tìm một điểm A bất kì nên mình có thể cho x bằng bao nhiêu cũng được, rồi từ đó tìm y và z tương ứng ta sẽ được một điểm tương ứng.
thầy ơi, em không hiểu chỗ thay để ra A(0,-3,-2) ạ, thầy nói rõ hơn chỗ đó được không ạ?
@Pathy giải hệ pt tổng quát của đen ta đấy bạn
Thầy ơi , điểm A(0;-3;-2) chứ ạ .
@Long Cảm ơn Long, là do thầy viết nhầm.
Tích có hướng sai rồi. Vecto pháp tuyến của Alpha phải là (1 ; 0 ; -1 ) chứ không phải là ( 3 ; 0 ; -1)
@Hùng cảm ơn bạn