Hình chiếu vuông góc của một điểm lên đường thẳng
Hình chiếu vuông góc của một điểm lên đường thẳng trong không gian. Cách tìm hình chiếu của một điểm lên đường thẳng trong không gian.
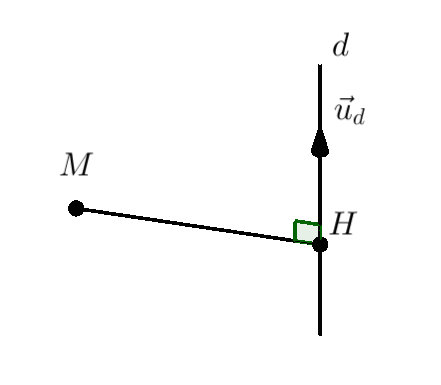
Bước 1. Viết phương trình của đường thẳng $d$ ở dạng tham số $$\left( d \right):\left\{ \begin{array}{l}
x = {x_0} + at\\
y = {y_0} + bt\\
z = {z_0} + ct
\end{array} \right.$$
Bước 2. Điểm $H \in d$ nên $H\left( {{x_0} + at,{y_0} + bt,{z_0} + ct} \right).$
Bước 3. Từ điều kiện $\overrightarrow {MH} \bot {\vec u_d} \Leftrightarrow \overrightarrow {MH} \cdot {\vec u_d} = 0$ ta lập phương trình và giải tìm $t$, thay vào phương trình của $d$ ta được toạ độ điểm $H$.
Ví dụ. Tìm toạ độ hình chiếu $H$ của điểm $M\left( {1;1;3} \right)$ lên đường thẳng $\left( d \right):\left\{ \begin{array}{l}
x = 1 - t\\
y = 2 + 2t\\
z = - 1 - t
\end{array} \right..$
Giải. Vì $H \in d \Rightarrow H\left( {1 - t;2 + 2t; - 1 - t} \right) \Rightarrow \overrightarrow {MH} = \left( { - t;1 + 2t; - 4 - t} \right).$ Mặt khác ${\vec u_d} = \left( { - 1;2; - 1} \right).$
$$\overrightarrow {MH} \bot {\vec u_d} \Leftrightarrow \overrightarrow {MH} \cdot {\vec u_d} = 0 \Leftrightarrow \left( { - t} \right) \cdot \left( { - 1} \right) + \left( {1 + 2t} \right) \cdot 2 + \left( { - 4 - t} \right) \cdot \left( { - 1} \right) = 0 \Leftrightarrow t = - 1.$$
Thay $t = - 1$ vào phương trình của $d$ ta được $x = 2;y = 0;z = 0.$
Vậy toạ độ hình chiếu $H$ của điểm $M$ lên đường thẳng $\left( d \right)$ là $H\left( { 2;0;0} \right).$
Bài tập
Tác giả bài viết: Cùng Học Toán
Góp ý hoặc một bài toán của Quý học viên hoặc Quý Phụ Huynh




chẳng hiểu jjjjjj