Tỷ mỷ làm toán. Độc lập suy nghĩ.
Tỷ mỷ làm toán. Độc lập suy nghĩ.
Khoảng cách từ một điểm đến một mặt phẳng
Khoảng cách từ một điểm đến một mặt phẳng. Công thức tính khoảng cách.
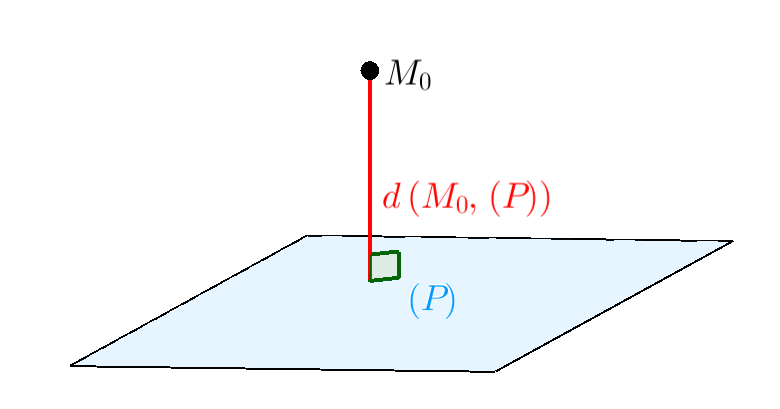
Khoảng cách từ điểm đến mặt phẳng. Khoảng cách từ điểm ${M_0}\left( {{x_0};{y_0};{z_0}} \right)$ đến mp $\left( P \right):Ax + By + Cz + D = 0,$ ký hiệu $d\left( {{M_0},\left( P \right)} \right),$ được tính theo công thức $$d\left( {{M_0},\left( P \right)} \right) = \frac{{\left| {A{x_0} + B{y_0} + C{z_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}.$$
Ví dụ 1. Tính khoảng cách từ điểm ${M_0}\left( {2;1; - 3} \right)$ đến mặt phẳng $\left( P \right):2x - y - 2z - 3 = 0.$
Giải. Ta có $$d\left( {{M_0},\left( P \right)} \right) = \frac{{\left| {2 \cdot 2 - 1 - 2\left( { - 3} \right) - 3} \right|}}{{\sqrt {{2^2} + {{\left( { - 1} \right)}^2} + {{\left( { - 2} \right)}^2}} }} = 2.$$
Tác giả bài viết: Cùng Học Toán
Góp ý hoặc một bài toán của Quý học viên hoặc Quý Phụ Huynh