Tỷ mỷ làm toán. Độc lập suy nghĩ.
Tỷ mỷ làm toán. Độc lập suy nghĩ.
Phương trình mặt phẳng
Phương trình tổng quát của mặt phẳng. Phương trình chính tắc của mặt phẳng. Phương trình đoạn chắn của mặt phẳng.
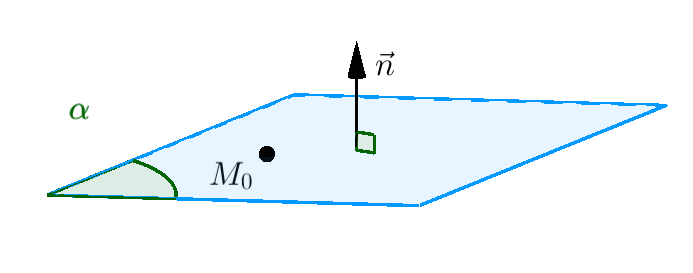
Ví dụ 1. Phương trình mặt phẳng $\left( \alpha \right)$ đi qua điểm $M\left( {2;1; - 3} \right)$ và có vector pháp tuyến $\vec n = \left( {4;2; - 1} \right)$ là
$$4\left( {x - 2} \right) + 2\left( {y - 1} \right) - 1\left( {z + 3} \right) = 0 \Leftrightarrow 4x + 2y - z - 9 = 0.$$
Ví dụ 2. Viết phương trình mặt phẳng $\left( \alpha \right)$ qua điểm ${M_0}\left( { - 1;1;2} \right)$ và vuông góc với trục $Ox$.
Giải. Ta có ${{\vec n}_\alpha } = \vec i = \left( {1;0;0} \right)$. Phương trình của mặt phẳng $\left( \alpha \right):$ $1\left( {x + 1} \right) + 0\left( {y - 1} \right) + 0\left( {z - 2} \right) = 0 \Leftrightarrow x + 1 = 0.$
Phương trình tổng quát của mặt phẳng. Mặt phẳng $\left( \alpha \right)$ có phương trình tổng quát dạng $Ax + By + Cz + D = 0$ và vector pháp tuyến là ${{\vec n}_\alpha } = \left( {A;B;C} \right) \ne \vec 0.$
Ví dụ 3. Giả sử mặt phẳng $\left( P \right):$ $x - 2y + 3z = 0.$ Xác định vector pháp tuyến và một điểm thuộc $\left( P \right)$.
Ví dụ 3. Giả sử mặt phẳng $\left( P \right):$ $x - 2y + 3z = 0.$ Xác định vector pháp tuyến và một điểm thuộc $\left( P \right)$.
Giải. Vector pháp tuyến của mặt phẳng $\left( P \right)$ là ${{\vec n}_P} = \left( {1; - 2;3} \right)$.
Thay $x = 1,{\rm{ }}y = 2$ vào phương trình của $\left( P \right)$ ta được $1 - 2 \cdot 2 + 3z = 0 \Rightarrow z = 1 \Rightarrow {M_0}\left( {1;2;1} \right) \in \left( P \right).$
Thay $x = 1,{\rm{ }}y = 2$ vào phương trình của $\left( P \right)$ ta được $1 - 2 \cdot 2 + 3z = 0 \Rightarrow z = 1 \Rightarrow {M_0}\left( {1;2;1} \right) \in \left( P \right).$
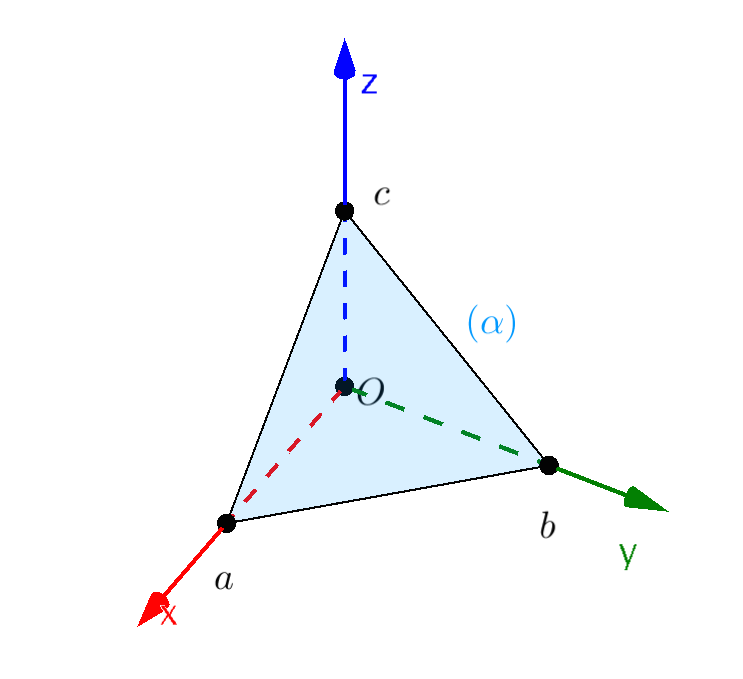
Phương trình mặt phẳng theo đoạn chắn. Mặt phẳng $\left( \alpha \right)$ đi cắt các trục toạ độ $Ox$, $Oy$, $Oz$ lần lượt ở $A\left( {a;0;0} \right),$ $B\left( {0;b;0} \right), C\left( {0;0;c} \right)$ sẽ có phương trình là $$\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1$$ và được gọi là phương trình theo đoạn chắn của $\left( \alpha \right)$.
Ví dụ 3. Viết phương trình tổng quát mặt phẳng đi qua ba điểm $A\left( {2;0;0} \right),B\left( {0; - 1;0} \right),C\left( {0;0;3} \right).$
Giải. Phương trình theo đoạn chắn
$$\frac{x}{2} + \frac{y}{{ - 1}} + \frac{z}{3} = 1 \Leftrightarrow 3x - 6y + 2z - 6 = 0.$$
Bài tập
Tác giả bài viết: Cùng Học Toán
Góp ý hoặc một bài toán của Quý học viên hoặc Quý Phụ Huynh