Tỷ mỷ làm toán. Độc lập suy nghĩ.
Tỷ mỷ làm toán. Độc lập suy nghĩ.
Vector chỉ phương của đường thẳng
Vector chỉ phương của đường thẳng. Cặp vector pháp tuyến của đường thẳng. Tích có hướng và vector chỉ phương của đường thẳng.
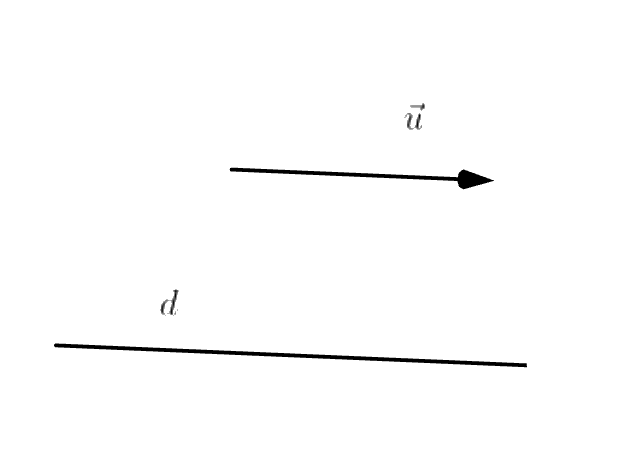
Nếu $\vec u$ là vector chỉ phương của $d$ thì với mọi số thực $k \ne 0$, vector $k \vec u$ cũng là một vector chỉ phương của $d$.
Như vậy mỗi đường thẳng sẽ có vô số các vector chỉ phương, và chúng có phương song song nhau.
Ví dụ 1. Nếu đường thẳng $d$ có vector chỉ phương là $\vec u = \left( {2;4;6} \right) = 2\left( {1;2;3} \right)$ thì $\vec u' = \left( {1;2;3} \right)$ cũng là vector chỉ phương của $d$.
Lưu ý là để đơn giản trong tính toán, người ta sẽ chọn vector chỉ phương có toạ độ càng đơn giản càng tốt. Chẳng hạn như trong Ví dụ 1, ta sẽ chọn $\vec u'$ mà không chọn $\vec u$.
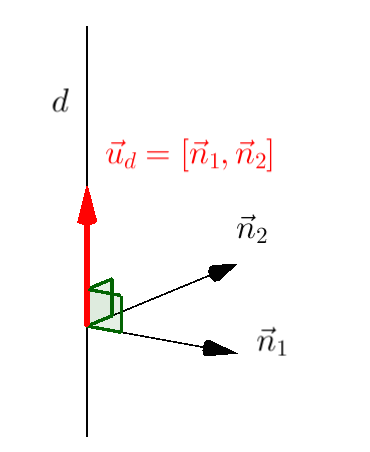
Cặp vector pháp tuyến của đường thẳng. Nếu hai vector ${{\vec n}_1},{{\vec n}_2}$ không không cùng phương và có phương vuông góc với đường thẳng $d$ thì hai vector này được gọi là cặp vector pháp tuyến của $d$.
Mệnh đề. Nếu ${{\vec n}_1},{{\vec n}_2}$ là một cặp vector pháp tuyến của đường thẳng $d$ thì vector chỉ phương của $d$ là $${{\vec u}_d} = \left[ {{{\vec n}_1},{{\vec n}_2}} \right].$$
Ví dụ 2. Xác định một vector chỉ phương của đường thẳng $d$ biết rằng đường thẳng này vuông góc với hai vector ${\vec n_1} = \left( { - 1;2;1} \right),{\vec n_2} = \left( {1;0;3} \right).$
Giải. Theo mệnh đề trên thì vector chỉ phương của $d$ là tích có hướng của ${{\vec n}_1}$ và ${{\vec n}_2}$:
$${{\vec u}_d} = \left[ {{{\vec n}_1},{{\vec n}_2}} \right] = \left( {\left| {\begin{array}{*{20}{c}}
2&1 \\
0&3
\end{array}} \right|; - \left| {\begin{array}{*{20}{c}}
{ - 1}&1 \\
1&3
\end{array}} \right|;\left| {\begin{array}{*{20}{c}}
{ - 1}&2 \\
1&0
\end{array}} \right|} \right) = \left( {6; - 4; - 2} \right).$$
$${{\vec u}_d} = \left[ {{{\vec n}_1},{{\vec n}_2}} \right] = \left( {\left| {\begin{array}{*{20}{c}}
2&1 \\
0&3
\end{array}} \right|; - \left| {\begin{array}{*{20}{c}}
{ - 1}&1 \\
1&3
\end{array}} \right|;\left| {\begin{array}{*{20}{c}}
{ - 1}&2 \\
1&0
\end{array}} \right|} \right) = \left( {6; - 4; - 2} \right).$$
Tác giả bài viết: Cùng Học Toán
Góp ý hoặc một bài toán của Quý học viên hoặc Quý Phụ Huynh