Hàm số liên tục
Hàm số liên tục. Hàm số liên tục tại một điểm. Hàm số liên tục trên một khoảng.
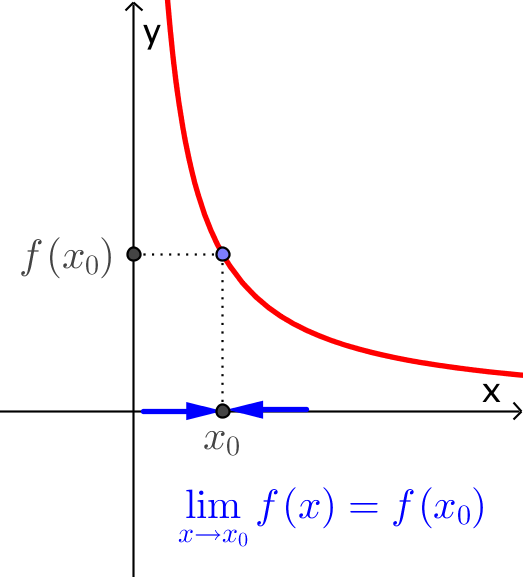
Hàm số liên tục tại một điểm. Cho hàm số $f\left( x \right)$ liên tục trên khoảng $\left( {a;b} \right)$ chứa $x_0$. Khi đó hàm số $f\left( x \right)$ được gọi là liên tục tại $x_0$ nếu $$\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)$$
Nếu hàm số $f\left( x \right)$ không liên tục tại $x_0$ thì ta nói $f\left( x \right)$ gián đoạn tại $x_0$ và $x_0$ được gọi là điểm gián đoạn.
Ví dụ 1. Hàm số $f\left( x \right) = {x^2}$ liên tục tại mọi điểm ${x_0} \in \mathbb{R}$ vì $$\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} {x^2} = x_0^2 = f\left( {{x_0}} \right).$$
Ví dụ 2. Xét tính liên tục của hàm số $f\left( x \right) = \left\{ \begin{gathered} \frac{{{x^2} - 1}}{{x - 1}},\;\;x \ne 1; \hfill \\ 3,\;\;\;\;\;\;\;\;\;x = 1. \hfill \\ \end{gathered} \right.$
Tập xác định $D = \mathbb{R}.$
Tại ${x_0} = 1,$ ta có $f\left( 1 \right) = 3,$ $\mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \left( {x + 1} \right) = 2.$
Vì $\mathop {\lim }\limits_{x \to 1} f\left( x \right) \ne f\left( 1 \right)$ nên hàm số gián đoạn tại ${x_0} = 1.$
Tại ${x_0} = 1,$ ta có $f\left( 1 \right) = 3,$ $\mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \left( {x + 1} \right) = 2.$
Vì $\mathop {\lim }\limits_{x \to 1} f\left( x \right) \ne f\left( 1 \right)$ nên hàm số gián đoạn tại ${x_0} = 1.$
Liên tục trái. Hàm số $f\left( x \right)$ được gọi là liên tục trái tại $x_0$ nếu $$\mathop {\lim }\limits_{x \to {x_0^-}} f\left( x \right) = f\left( {{x_0}} \right).$$
Liên tục phải. Hàm số $f\left( x \right)$ được gọi là liên tục phải tại $x_0$ nếu $$\mathop {\lim }\limits_{x \to {x_0^+}} f\left( x \right) = f\left( {{x_0}} \right).$$
Ví dụ 3.
Bình luận 1. Như vậy, có hàm số liên tục trái nhưng không liên tục phải; ngược lại, có những hàm số liên tục phải nhưng không liên tục trái. Tuy nhiên từ định nghĩa, nếu hàm số liên tục tại một điểm thì sẽ liên tục trái và liên tục phải tại điểm đó. Ta có mệnh đề sau
Hàm số liên tục trên một khoảng. Hàm số $f\left( x \right)$ được gọi là liên tục trên khoảng $\left( {a;b} \right)$ nếu nó liên tục tại mọi điểm $x_0$ thuộc khoảng $\left( {a;b} \right)$.
Hàm số liên tục tại một điểm. Hàm số $f\left( x \right)$ được gọi là liên tục trên đoạn $\left[ {a;b} \right]$ nếu $f\left( x \right)$ liên tục trên khoảng $\left( {a;b} \right)$, liên tục phải tại $a$ và liên tục trái tại $b$.
Liên tục phải. Hàm số $f\left( x \right)$ được gọi là liên tục phải tại $x_0$ nếu $$\mathop {\lim }\limits_{x \to {x_0^+}} f\left( x \right) = f\left( {{x_0}} \right).$$
Ví dụ 3.
Bình luận 1. Như vậy, có hàm số liên tục trái nhưng không liên tục phải; ngược lại, có những hàm số liên tục phải nhưng không liên tục trái. Tuy nhiên từ định nghĩa, nếu hàm số liên tục tại một điểm thì sẽ liên tục trái và liên tục phải tại điểm đó. Ta có mệnh đề sau
|
Hàm số $f\left( x \right)$ liên tục tại $x_0$ khi và chỉ khi $f\left( x \right)$ liên tục trái và liên tục phải tại $x_0$.
|
Hàm số liên tục trên một khoảng. Hàm số $f\left( x \right)$ được gọi là liên tục trên khoảng $\left( {a;b} \right)$ nếu nó liên tục tại mọi điểm $x_0$ thuộc khoảng $\left( {a;b} \right)$.
Hàm số liên tục tại một điểm. Hàm số $f\left( x \right)$ được gọi là liên tục trên đoạn $\left[ {a;b} \right]$ nếu $f\left( x \right)$ liên tục trên khoảng $\left( {a;b} \right)$, liên tục phải tại $a$ và liên tục trái tại $b$.
Tác giả bài viết: Cùng Học Toán




Góp ý hoặc một bài toán của Quý học viên hoặc Quý Phụ Huynh