Tỷ mỷ làm toán. Độc lập suy nghĩ.
Tỷ mỷ làm toán. Độc lập suy nghĩ.
Bài toán giao tuyến: đi qua hai điểm
Cách xác định giao tuyến của hai mặt phẳng. Xác định giao tuyến đi qua hai điểm.
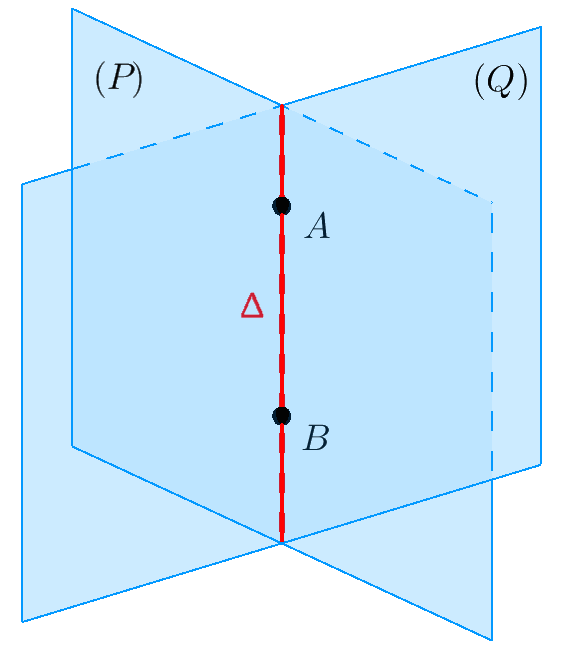
Giao tuyến. Nếu hai mặt phẳng $(P)$ và $(Q)$ cắt nhau theo đường thẳng $\Delta$ thì đường thẳng này được gọi là giao tuyến của $(P)$ và $(Q)$. Khi đó ta cũng viết $\Delta = \left( P \right) \cap \left( Q \right)$.
Trong bài này sẽ bàn đến bài toán tìm giao tuyến bằng cách xác định hai điểm phân biệt mà giao tuyến này đi qua.
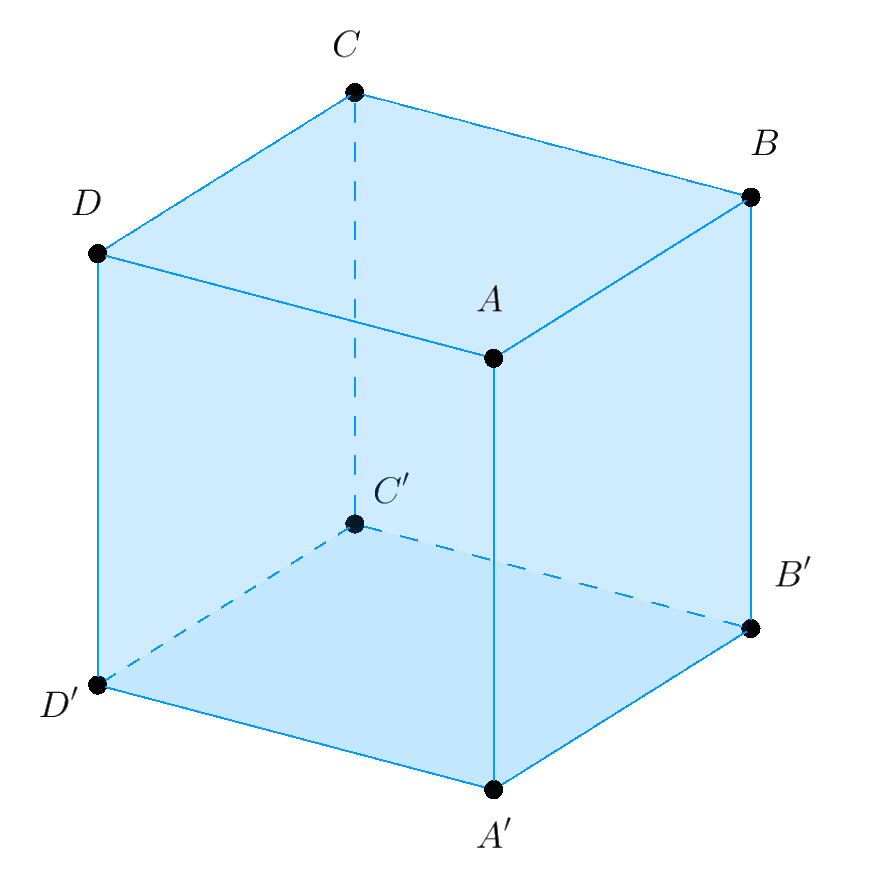
Ví dụ 1. Hãy xác định giao tuyến của hai mặt $\left( {ABCD} \right)$ và $\left( {ABB'A'} \right)$. Rõ ràng $A$ và $B$ là hai điểm chung phân biệt của hai mặt phẳng này. Như vậy $$\left( {ABCD} \right) \cap \left( {ABB'A'} \right) = AB.$$
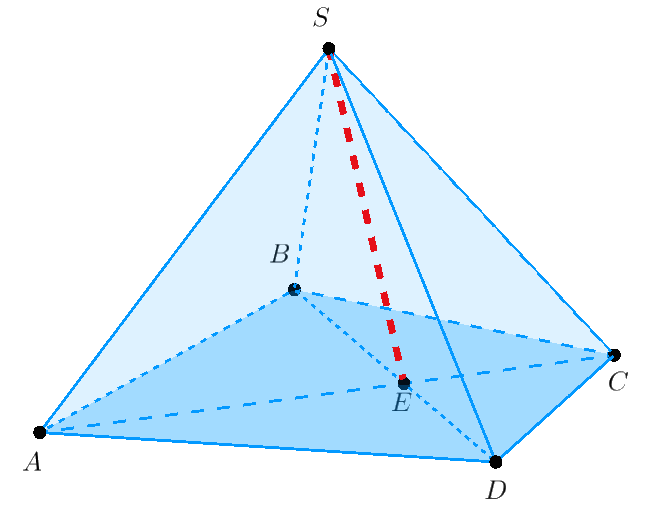
Ví dụ 2. Cho hình chóp $S.ABCD$. Hãy xác định giao tuyến giữa hai mặt $\left( {SAC} \right)$ và $\left( {SBD} \right)$.
Giải. Trong mặt phẳng $\left( {ABCD} \right)$ gọi $E = AC \cap BD.$ Khi đó ta có $$\left. \begin{gathered}
E \in AC \subset \left( {SAC} \right) \hfill \\
E \in BD \subset \left( {SBC} \right) \hfill \\
\end{gathered} \right\} \Rightarrow E \in \left( {SAC} \right) \cap \left( {SBC} \right)\,\,\,\,\,\,\left( 1 \right).$$ Hiển nhiên ta có $S \in \left( {SAC} \right) \cap \left( {SBC} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)$
Từ $\left( 1 \right)\& \left( 2 \right)$ suy ra $SE = \left( {SAC} \right) \cap \left( {SBC} \right).$
E \in AC \subset \left( {SAC} \right) \hfill \\
E \in BD \subset \left( {SBC} \right) \hfill \\
\end{gathered} \right\} \Rightarrow E \in \left( {SAC} \right) \cap \left( {SBC} \right)\,\,\,\,\,\,\left( 1 \right).$$ Hiển nhiên ta có $S \in \left( {SAC} \right) \cap \left( {SBC} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)$
Từ $\left( 1 \right)\& \left( 2 \right)$ suy ra $SE = \left( {SAC} \right) \cap \left( {SBC} \right).$
Ví dụ 3. Cho hình chóp $S.ABCD$ có $AB > CD$. Xác định giao tuyến của hai mặt phẳng $\left( {SBC} \right)$ và $\left( {SAD} \right).$
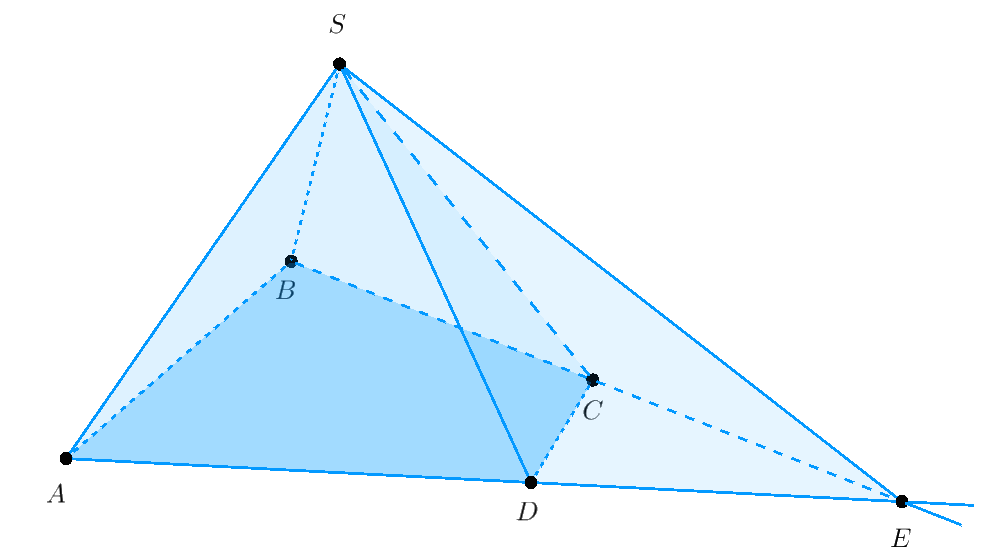
Giải. Trong mặt phẳng đáy $\left( {ABCD} \right)$ gọi $E = AD \cap BC.$ Ta có
$$\left. \begin{gathered}
E \in BC \subset \left( {SBC} \right) \hfill \\
E \in AD \subset \left( {SAD} \right) \hfill \\
\end{gathered} \right\} \Rightarrow E \in \left( {SBC} \right) \cap \left( {SAD} \right)\,\,\,\,\left( 1 \right)$$
E \in BC \subset \left( {SBC} \right) \hfill \\
E \in AD \subset \left( {SAD} \right) \hfill \\
\end{gathered} \right\} \Rightarrow E \in \left( {SBC} \right) \cap \left( {SAD} \right)\,\,\,\,\left( 1 \right)$$
Hiển nhiên ta có $S \in \left( {SBC} \right) \cap \left( {SAD} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)$
Từ $\left( 1 \right)\& \left( 2 \right)$ suy ra $SE = \left( {SBC} \right) \cap \left( {SAD} \right)\,.$
Từ $\left( 1 \right)\& \left( 2 \right)$ suy ra $SE = \left( {SBC} \right) \cap \left( {SAD} \right)\,.$
Bài tập
Tác giả bài viết: Cùng Học Toán
Góp ý hoặc một bài toán của Quý học viên hoặc Quý Phụ Huynh