Tỷ mỷ làm toán. Độc lập suy nghĩ.
Tỷ mỷ làm toán. Độc lập suy nghĩ.
Bài toán thiết diện: vuông góc với một đường
Xác định thiết diện vuông góc với một đường thẳng cho trước
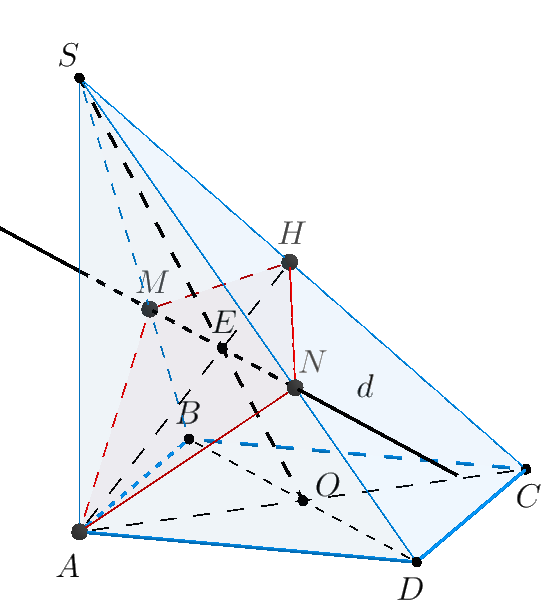
Ví dụ. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, $SA \bot \left( {ABCD} \right).$ Gọi $\left( \alpha \right)$ là mặt phẳng qua $A$ vuông góc với $SC.$ Xác định thiết diện của hình chóp cắt bởi $\left( \alpha \right).$
Giải. Giả sử $\left( \alpha \right)$ cắt $SC$ tại $H$. Khi đó $AH \subset \left( \alpha \right) \bot SC \Rightarrow AH \bot SC.$
Vì $BD \bot \left( {SAC} \right)$ nên $BD \bot SC.$ $\left( 1 \right)$
Mà $\left( \alpha \right) \bot SC.$ $\left( 2 \right)$
Từ $\left( 1 \right)\& \left( 2 \right) \Rightarrow \left( \alpha \right)\parallel BD.$
$ \Rightarrow \left( \alpha \right) \cap \left( {SBD} \right) = d\parallel BD.$
Mặt khác gọi $E = AH \cap SO \Rightarrow E \in d.$
Vậy $d$ là đường thẳng đi qua $E$, song song với $BD$ và lần lượt cắt $SB,SD$ tại $M,N$.
Vậy thiết diện cần tìm là tứ giác $AMHN.$
Vì $BD \bot \left( {SAC} \right)$ nên $BD \bot SC.$ $\left( 1 \right)$
Mà $\left( \alpha \right) \bot SC.$ $\left( 2 \right)$
Từ $\left( 1 \right)\& \left( 2 \right) \Rightarrow \left( \alpha \right)\parallel BD.$
$ \Rightarrow \left( \alpha \right) \cap \left( {SBD} \right) = d\parallel BD.$
Mặt khác gọi $E = AH \cap SO \Rightarrow E \in d.$
Vậy $d$ là đường thẳng đi qua $E$, song song với $BD$ và lần lượt cắt $SB,SD$ tại $M,N$.
Vậy thiết diện cần tìm là tứ giác $AMHN.$
Tác giả bài viết: Cùng Học Toán
Góp ý hoặc một bài toán của Quý học viên hoặc Quý Phụ Huynh