Đại cương về đường thẳng và mặt phẳng
Các quy tắc biễu diễn một hình không gian trong mặt giấy
Một số ký hiệu nên lưu ý.

|
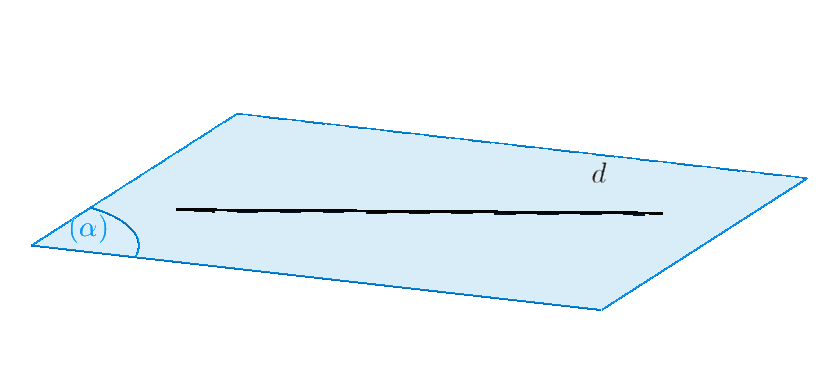
$ \bullet $ Nếu điểm $A$ thuộc đường thẳng $d$ ta ký hiệu $A \in a$, đôi khi ta cũng nói đường thẳng $ d$ đi qua điểm $A$. |
|
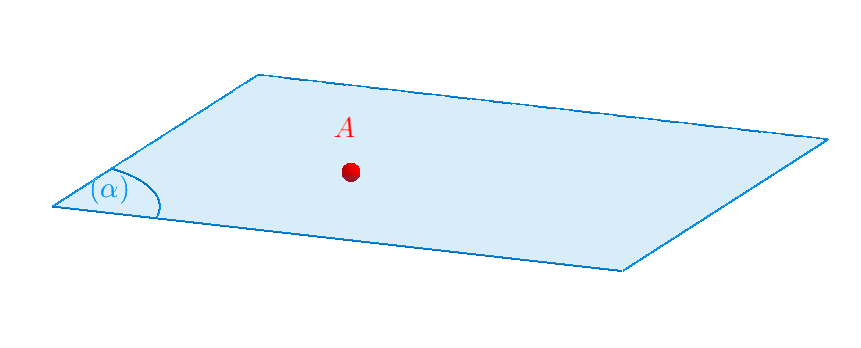
$ \bullet $ Nếu điểm $A$ thuộc mặt phẳng $ (\alpha) $ ta ký hiệu $A \in (\alpha)$, ta cũng nói mặt phẳng $ (\alpha) $ đi qua điểm $A$. |
|
$ \bullet $ Nếu đường thẳng $d$ chứa trong mặt phẳng $ (\alpha) $ ta ký hiệu $ d \subset \left( \alpha \right)$, ta cũng nói mặt phẳng $ \left( \alpha \right)$ đi qua hay chứa đường thẳng $ d $. |
Một số quy tắc biểu diễn các đối tượng trong không gian.
$ \bullet $ Hình biểu diễn của đường thẳng là đường thẳng, của đoạn thẳng là đoạn thẳng.
$ \bullet $ Hình biểu diễn của hai đường thẳng song song là hai đường thẳng song song, của hai đường thẳng cắt nhau là hai đường thẳng cắt nhau.
$ \bullet $ Hình biểu diễn phải đảm bảo quan hệ thuộc giữa điểm, đường thẳng, và mặt phẳng.
$ \bullet $ Dùng nét vẽ liền để biểu diễn cho đường nhìn thấy, và nét đứt để biểu diễn cho đường bị che khuất.
$ \bullet $ Hình biểu diễn của hai đường thẳng song song là hai đường thẳng song song, của hai đường thẳng cắt nhau là hai đường thẳng cắt nhau.
$ \bullet $ Hình biểu diễn phải đảm bảo quan hệ thuộc giữa điểm, đường thẳng, và mặt phẳng.
$ \bullet $ Dùng nét vẽ liền để biểu diễn cho đường nhìn thấy, và nét đứt để biểu diễn cho đường bị che khuất.
Tác giả bài viết: Cùng Học Toán




Góp ý hoặc một bài toán của Quý học viên hoặc Quý Phụ Huynh