Định lý Thales trong không gian
Định lý thales trong không gian. Định lý đảo của định lý Thales trong không gian. Ứng dụng của định lý Thales trong không gian.
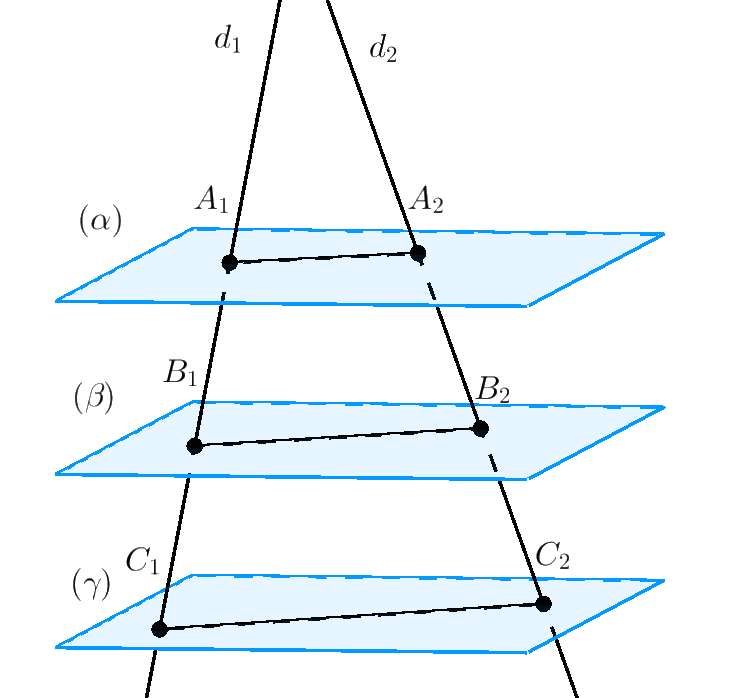
Định lý Thales trong không gian. Ba mặt phẳng song song chắn trên hai đường thẳng những đoạn thẳng tỷ lệ. $$\frac{{{A_1}{B_1}}}{{{B_1}{C_1}}} = \frac{{{A_2}{B_2}}}{{{B_2}{C_2}}}.$$
Định lý đảo của định lý Thales trong không gian. Cho hai đường thẳng ${d_1},{d_2}$ chéo nhau và các điểm ${A_1},{B_1},{C_1} \in {d_1},$ và ${A_2},{B_2},{C_2} \in {d_2}$ sao cho $$\frac{{{A_1}{B_1}}}{{{B_1}{C_1}}} = \frac{{{A_2}{B_2}}}{{{B_2}{C_2}}}.$$ Khi đó các đường thẳng ${A_1}{A_2},{B_1}{B_2},{C_1}{C_2}$ cùng song song với một mặt phẳng. Hơn nữa, mặt phẳng này không duy nhất.
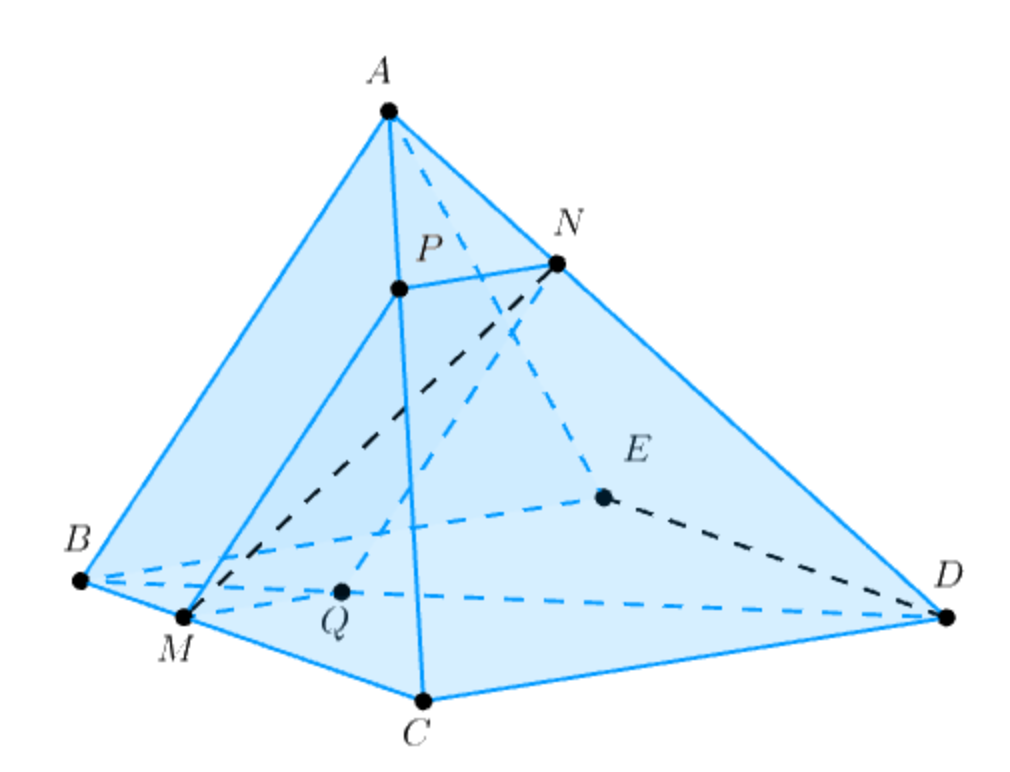
Ví dụ. Cho tứ diện $ABCD$ và $M,N$ là các điểm lần lượt di động trên $BC,AD$ sao cho $\frac{{BM}}{{MC}} = \frac{{AN}}{{ND}}.$ Chứng minh rằng $MN$ luôn song song với một mặt phẳng cố định.
Giải. Áp dụng định lý Thales đảo cho $B,M,C \in BC$ và $A,N,D \in AD$ , từ tỷ lệ $$\frac{{BM}}{{MC}} = \frac{{AN}}{{ND}}$$ ta suy ra $AB,MN,CD$ cùng song song với một mặt phẳng $\left( \pi \right)$ nào đó.
Ta chọn mặt phẳng $\left( \alpha \right)$ chứa $AB$ và song song với $CD.$ Mặt phẳng $\left( \alpha \right)$ chính là $\left( {ABE} \right)$ với $E \in \left( {BCD} \right)$ sao cho $BCDE$ là hình bình hành.
Khi đó $MN\parallel \left( \pi \right)\parallel \left( \alpha \right),$ mặt phẳng $\left( \alpha \right)$ cố định vì $AB,CD$ cố định. Vậy $\left( \alpha \right)$ là mặt phẳng cần tìm.
Ta chọn mặt phẳng $\left( \alpha \right)$ chứa $AB$ và song song với $CD.$ Mặt phẳng $\left( \alpha \right)$ chính là $\left( {ABE} \right)$ với $E \in \left( {BCD} \right)$ sao cho $BCDE$ là hình bình hành.
Khi đó $MN\parallel \left( \pi \right)\parallel \left( \alpha \right),$ mặt phẳng $\left( \alpha \right)$ cố định vì $AB,CD$ cố định. Vậy $\left( \alpha \right)$ là mặt phẳng cần tìm.
Tác giả bài viết: Cùng Học Toán




Góp ý hoặc một bài toán của Quý học viên hoặc Quý Phụ Huynh