Tỷ mỷ làm toán. Độc lập suy nghĩ.
Tỷ mỷ làm toán. Độc lập suy nghĩ.
Hai mặt phẳng vuông góc
Hai mặt phẳng vuông góc. Cách chứng minh hai mặt phẳng vuông góc
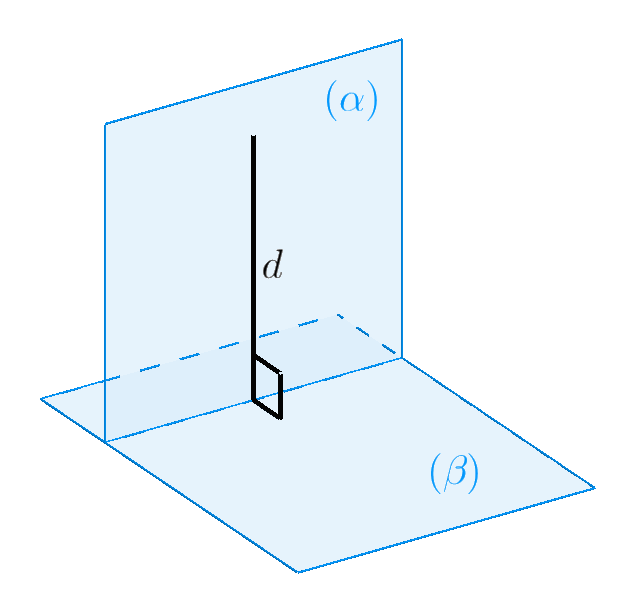
Định lý. Hai mặt phẳng vuông góc với nhau khi và chỉ khi mặt này chứa một đường vuông góc với mặt kia. $$\left. \begin{gathered}
\left( \alpha \right) \supset a \hfill \\
a \bot \left( \beta \right) \hfill \\
\end{gathered} \right\} \Rightarrow \left( \alpha \right) \bot \left( \beta \right).$$
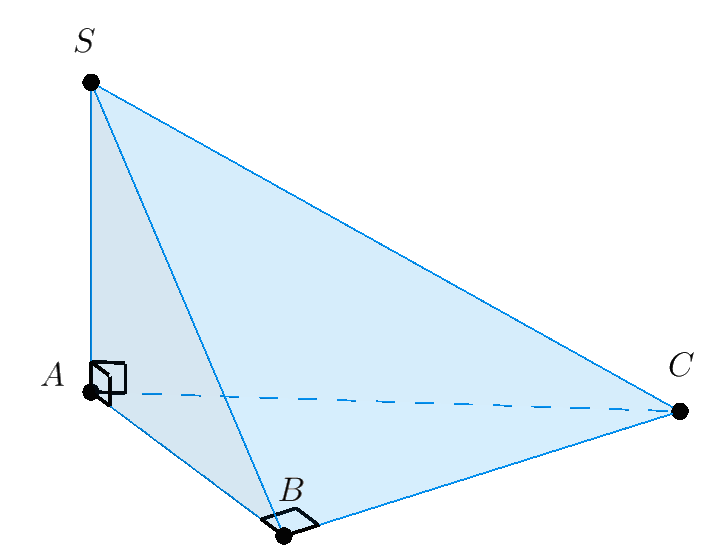
Ví dụ. Cho hình chóp tam giác $S.ABC$ có đáy là tam giác vuông tại $B$, $SA \bot \left( {ABC} \right).$ Gọi $BH$ là đường cao của $\Delta ABC.$ Chứng minh $\left( {SAB} \right) \bot \left( {ABC} \right)$ và $\left( {SBC} \right) \bot \left( {SAB} \right).$
Giải. Ta có $\left. \begin{gathered}
SA \subset \left( {SAB} \right) \hfill \\
SA \bot \left( {ABC} \right) \hfill \\
\end{gathered} \right\} \Rightarrow \left( {SAB} \right) \bot \left( {ABC} \right).$
Ta có
$\left. \begin{gathered}
SA \bot \left( {ABC} \right) \hfill \\
BC \subset \left( {ABC} \right) \hfill \\
\end{gathered} \right\} \Rightarrow SA \bot BC\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( 1 \right)$
Mặt khác từ giả thiết ta có $BC \bot AB\;\;\;\;\;\;\;\;\;\;\left( 2 \right)$
Từ $\left( 1 \right)\& \left( 2 \right) \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow \left( {SBC} \right) \bot \left( {SAB} \right).$
SA \subset \left( {SAB} \right) \hfill \\
SA \bot \left( {ABC} \right) \hfill \\
\end{gathered} \right\} \Rightarrow \left( {SAB} \right) \bot \left( {ABC} \right).$
Ta có
$\left. \begin{gathered}
SA \bot \left( {ABC} \right) \hfill \\
BC \subset \left( {ABC} \right) \hfill \\
\end{gathered} \right\} \Rightarrow SA \bot BC\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( 1 \right)$
Mặt khác từ giả thiết ta có $BC \bot AB\;\;\;\;\;\;\;\;\;\;\left( 2 \right)$
Từ $\left( 1 \right)\& \left( 2 \right) \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow \left( {SBC} \right) \bot \left( {SAB} \right).$
Bài tập
Tác giả bài viết: Cùng Học Toán
Góp ý hoặc một bài toán của Quý học viên hoặc Quý Phụ Huynh