Tỷ mỷ làm toán. Độc lập suy nghĩ.
Tỷ mỷ làm toán. Độc lập suy nghĩ.
Vị trí tương đối của đường thẳng và đường thẳng
Vị trí tương đối của đường thẳng và đường thẳng trong không gian
Vị trí tương đối của đường thẳng và đường thẳng. Trong không gian cho hai đường thẳng $d_1$ và $d_2$. Khi đó có $3$ vị trí tương đối giữa hai đường thẳng này
|
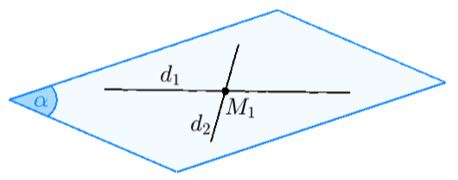
$\left( 1 \right)$ Đường thẳng ${d_1}$ và ${d_2}$ cắt nhau tại một điểm $M$. Khi đó tồn tại một mặt phẳng $\left( \alpha \right)$ chứa cả hai đường thẳng này. Ở trường hợp này thì ${d_1}$ và ${d_2}$ đồng phẳng $\hbox{ (cùng thuộc }$ $ \left( \alpha \right))$. |
|
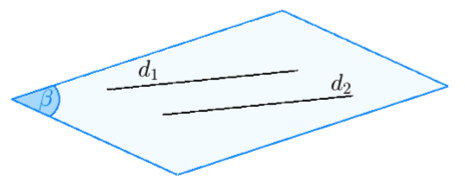
$\left( 2 \right)$ Trường hợp ${d_1}\parallel {d_2}$. Khi đó tồn tại mặt phẳng $\left( \beta \right)$ chứa cả hai đường thẳng này. Ở trường hợp này thì ${d_1}$ và ${d_2}$ đồng phẳng $\hbox{ (cùng thuộc }$ $ \left( \beta \right))$. |
|
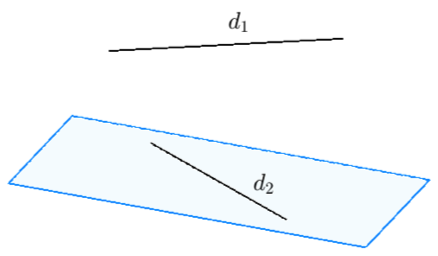
$\left( 3 \right)$ Đường thẳng ${d_1}$ và ${d_2}$ chéo nhau. Khi đó không tồn tại mặt phẳng chứa cả hai đường thẳng này. Ở trường hợp này thì ${d_1}$ và ${d_2}$ không đồng phẳng. |
Bài tập
Tác giả bài viết: Cùng Học Toán
Góp ý hoặc một bài toán của Quý học viên hoặc Quý Phụ Huynh