Tỷ mỷ làm toán. Độc lập suy nghĩ.
Tỷ mỷ làm toán. Độc lập suy nghĩ.
Cực trị
Cực trị của hàm số. Điều kiện để hàm số có cực trị. Điều kiện để hàm số đạt cực trị tại một điểm cho trước.
Định nghĩa cực trị. Cho hàm số $f\left( x \right) $ trên khoảng $\left( {a;b} \right)$ đủ nhỏ chưa điểm $x_0$.
Dấu "=" ở các bất đẳng thức trên chỉ được xảy ra ở một số hữu hạn điểm thuộc khoảng $\left( {a;b} \right)$. |
Ví dụ 1. Xét hàm số $f\left( x \right) = {x^2} - x + 1$.
Tập xác định $D = \mathbb{R}$, và với mọi $x \in D$ ta có $$f\left( x \right) = {x^2} - x + 1 = \left( {{x^2} - 2 \cdot x \cdot \frac{1}{2} + \frac{1}{4}} \right) + \frac{3}{4} = \underbrace {{{\left( {x - \frac{1}{2}} \right)}^2}}_{ \geqslant 0} + \frac{3}{4} \geqslant \frac{3}{4}.$$
Dấu $=$ xảy ra khi và chỉ khi $x = \frac{1}{2} \Rightarrow y = \frac{3}{4}$.
Từ đánh giá trên ta thấy trong một khoảng đủ nhỏ $\left( {a;b} \right)$ chứa $x_0=\frac{1}{2}$, ta luôn có $f\left( x \right) \ge f\left( {{x_0}} \right) = f\left( {\frac{1}{2}} \right) = \frac{3}{4}$ nên theo định nghĩa, hàm số đạt cực tiểu tại $x_0=\frac{1}{2}$, giá trị cực tiểu tương ứng là $y_0=\frac{3}{4}$. Điểm cực trị ${M_0}\left( {\frac{1}{2};\frac{3}{4}} \right).$
Dấu $=$ xảy ra khi và chỉ khi $x = \frac{1}{2} \Rightarrow y = \frac{3}{4}$.
Từ đánh giá trên ta thấy trong một khoảng đủ nhỏ $\left( {a;b} \right)$ chứa $x_0=\frac{1}{2}$, ta luôn có $f\left( x \right) \ge f\left( {{x_0}} \right) = f\left( {\frac{1}{2}} \right) = \frac{3}{4}$ nên theo định nghĩa, hàm số đạt cực tiểu tại $x_0=\frac{1}{2}$, giá trị cực tiểu tương ứng là $y_0=\frac{3}{4}$. Điểm cực trị ${M_0}\left( {\frac{1}{2};\frac{3}{4}} \right).$
Ví dụ 2. Xét hàm số $f\left( x \right) = \sqrt {x - 1} + \sqrt {2 - x} $.
Giải. Điều kiện xác định $$\left\{ \begin{gathered}
x - 1 \geqslant 0 \hfill \\
2 - x \geqslant 0 \hfill \\
\end{gathered} \right. \Leftrightarrow 1 \leqslant x \leqslant 2$$ Suy ra tập xác định $D = \left[ {1;2} \right]$. Áp dụng bất đẳng thức Cauchy - Swartz với mọi $x \in \left( {1;2} \right)$ ta có $$f\left( x \right) = \sqrt {x - 1} + \sqrt {2 - x} \leqslant \sqrt {{{\left( {\sqrt {x - 1} } \right)}^2} + {{\left( {\sqrt {2 - x} } \right)}^2}} \sqrt {{1^2} + {1^2}} = \sqrt 2. $$
Dấu $=$ xảy ra khi $x - 1 = 2 - x \Leftrightarrow x = \frac{3}{2}$.
Trong một khoảng đủ nhỏ $\left( {a;b} \right) \subset \left[ {1;2} \right]$ chứa $x_0=\frac{3}{2}$, ta luôn có $f\left( x \right) \geqslant f\left( {{x_0}} \right) = f\left( {\frac{3}{2}} \right) = \sqrt 2 $ nên theo định nghĩa, trên khoảng $\left( {1;2} \right)$ hàm số đạt cực đại tại ${x_0} = \frac{3}{2}$, giá trị cực đại tương ứng là $f\left( {{x_0}} \right) = \sqrt 2 .$
Lưu ý. Trên một khoảng $\left( {a;b} \right)$ thì giá trị cực đại của hàm số $f\left( x \right) $ có thể không trùng với giá trị lớn nhất; cũng tương tự giá trị giá trị cực tiểu có thể không trùng với giá trị nhỏ nhất. Vấn đề này được thảo luận kĩ hơn ở đây.x - 1 \geqslant 0 \hfill \\
2 - x \geqslant 0 \hfill \\
\end{gathered} \right. \Leftrightarrow 1 \leqslant x \leqslant 2$$ Suy ra tập xác định $D = \left[ {1;2} \right]$. Áp dụng bất đẳng thức Cauchy - Swartz với mọi $x \in \left( {1;2} \right)$ ta có $$f\left( x \right) = \sqrt {x - 1} + \sqrt {2 - x} \leqslant \sqrt {{{\left( {\sqrt {x - 1} } \right)}^2} + {{\left( {\sqrt {2 - x} } \right)}^2}} \sqrt {{1^2} + {1^2}} = \sqrt 2. $$
Dấu $=$ xảy ra khi $x - 1 = 2 - x \Leftrightarrow x = \frac{3}{2}$.
Trong một khoảng đủ nhỏ $\left( {a;b} \right) \subset \left[ {1;2} \right]$ chứa $x_0=\frac{3}{2}$, ta luôn có $f\left( x \right) \geqslant f\left( {{x_0}} \right) = f\left( {\frac{3}{2}} \right) = \sqrt 2 $ nên theo định nghĩa, trên khoảng $\left( {1;2} \right)$ hàm số đạt cực đại tại ${x_0} = \frac{3}{2}$, giá trị cực đại tương ứng là $f\left( {{x_0}} \right) = \sqrt 2 .$
Bây giờ ta sẽ nói đến một công cụ khác để tìm cực trị của hàm số
Mệnh đề. Cho hàm số $f\left( x \right) $ trên khoảng $\left( {a;b} \right)$ chưa điểm $x_0$. Nếu khi đi qua $x_0$ mà $f'\left( x \right)$ đổi dấu thì hàm số đạt cực trị tại $x_0$. Cụ thể, theo chiều từ trái sang phải
|
Bây giờ ta dùng lại Mệnh đề này để tìm cực trị của các hàm số ở Ví dụ 1 và Ví dụ 2.
Ví dụ 3. Tìm các điểm cực trị của hàm số $f\left( x \right) = {x^2} - x + 1$.
Giải. Tập xác định $D = \mathbb{R}$. Ta có $f'\left( x \right) = 2x - 1$; $$f'\left( x \right) = 0 \Leftrightarrow 2x - 1 = 0 \Leftrightarrow x = \frac{1}{2}$$ Với $x = \frac{1}{2} \Rightarrow y = \frac{3}{4}$ Bảng biến thiên
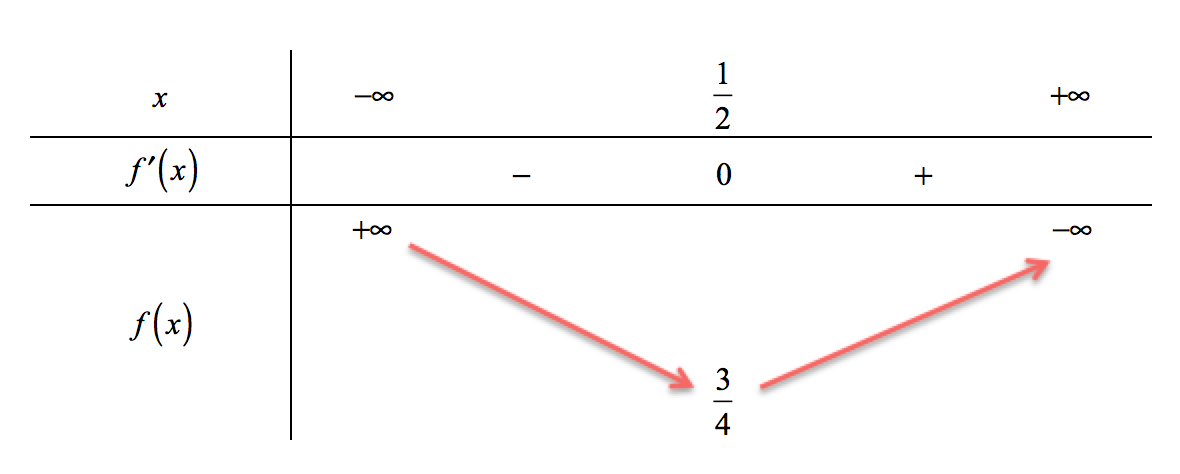
Ta thấy khi đi qua $x_0=\frac{1}{2}$ thì $f'\left( x \right)$ đổi từ $\left( - \right)$ thành $\left( + \right)$ nên $f\left( x \right) $ đạt cực tiểu tại $x_0=\frac{1}{2}$, giá trị cực tiểu tương ứng là $y_0=\frac{3}{4}$.
Ví dụ 4. Tìm cực trị của hàm số $f\left( x \right) = \sqrt {x - 1} + \sqrt {2 - x} $.
Ta thấy khi đi qua $x_0=\frac{1}{2}$ thì $f'\left( x \right)$ đổi từ $\left( - \right)$ thành $\left( + \right)$ nên $f\left( x \right) $ đạt cực tiểu tại $x_0=\frac{1}{2}$, giá trị cực tiểu tương ứng là $y_0=\frac{3}{4}$.
Giải. Tập xác định $D = \left[ {1;2} \right]$. Ta có $f'\left( x \right) = {1 \over 2}\left( {{1 \over {\sqrt {x - 1} }} - {1 \over {\sqrt {2 - x} }}} \right).$
$$f'\left( x \right) = 0 \Leftrightarrow \sqrt {x - 1} = \sqrt {2 - x} \Leftrightarrow x = {3 \over 2}.$$ Ta cũng có $\eqalign{
& x = {1 \over 2} \Rightarrow y = \sqrt 2 \cr
& x = 1 \Rightarrow y = 1 \cr
& x = 2 \Rightarrow y = 1 \cr} $.
Bảng biên thiên
Bàng cách thay một giá trị trong khoảng $\left( {{3 \over 2};2} \right)$ vào hàm số $f'\left( x \right) $ ta thấy $f'\left( x \right) $ mang dấu âm trên khoảng này. Làm tương tự ta có $f'\left( x \right) $ mang dấu dương tên khoảng $\left( {1;{3 \over 2}} \right)$.
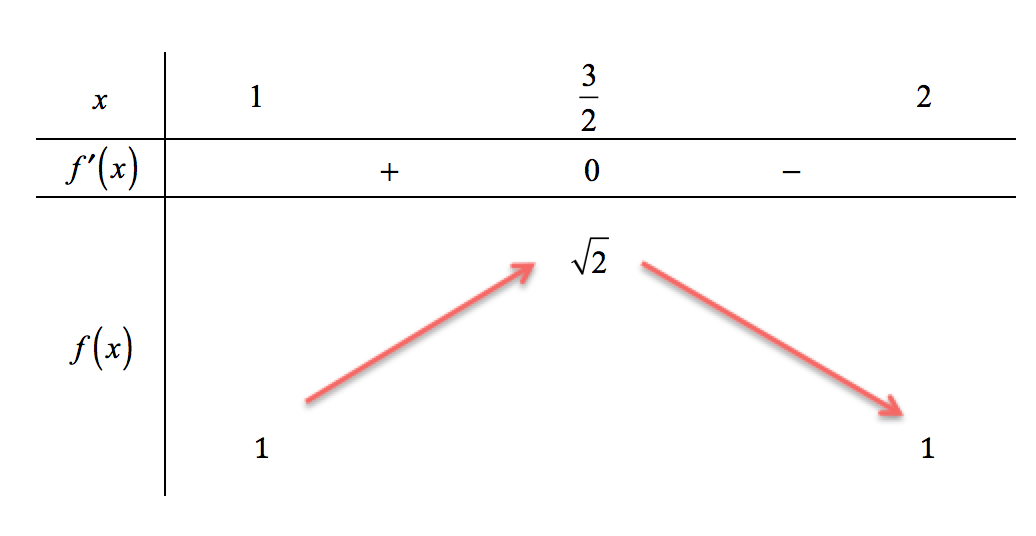
Từ bảng biến thiên ta suy ra hàm số đạt cực đại tại ${x_0} = \frac{3}{2}$ trên khoảng $\left( {1;2} \right)$, giá trị cực đại tương ứng là $f\left( {{x_0}} \right) = \sqrt 2 .$
Ví dụ 5. Tìm cực trị của hàm số $f\left( x \right) = {x^3} - 3{x^2} + 1$ trên đoạn $\left[ {0;4} \right]$.
$$f'\left( x \right) = 0 \Leftrightarrow \sqrt {x - 1} = \sqrt {2 - x} \Leftrightarrow x = {3 \over 2}.$$ Ta cũng có $\eqalign{
& x = {1 \over 2} \Rightarrow y = \sqrt 2 \cr
& x = 1 \Rightarrow y = 1 \cr
& x = 2 \Rightarrow y = 1 \cr} $.
Bảng biên thiên
Bàng cách thay một giá trị trong khoảng $\left( {{3 \over 2};2} \right)$ vào hàm số $f'\left( x \right) $ ta thấy $f'\left( x \right) $ mang dấu âm trên khoảng này. Làm tương tự ta có $f'\left( x \right) $ mang dấu dương tên khoảng $\left( {1;{3 \over 2}} \right)$.
Từ bảng biến thiên ta suy ra hàm số đạt cực đại tại ${x_0} = \frac{3}{2}$ trên khoảng $\left( {1;2} \right)$, giá trị cực đại tương ứng là $f\left( {{x_0}} \right) = \sqrt 2 .$
Giải. Tập xác định $D = \mathbb{R}$. Ta có $f'\left( x \right) = 3{x^2} - 6x$. Suy ra $$f'\left( x \right) = 0 \Leftrightarrow 3{x^2} - 6x = 0 \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
x = 2 \hfill \\
\end{gathered} \right..$$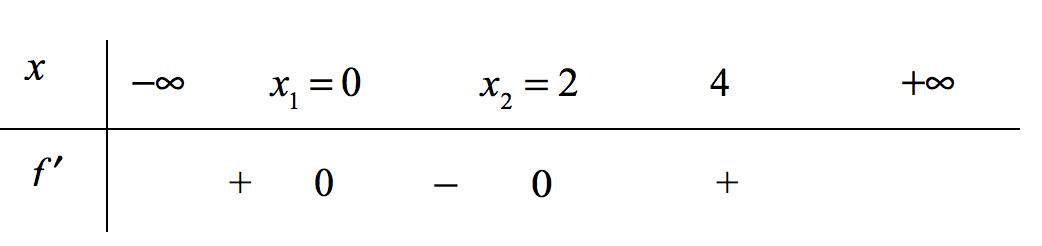
Bảng xét dấu của $f'\left( x \right) $ trên đoạn $D$
Trên đoạn $\left[ {0;4} \right]$ không tồn tại một khoảng nào chứa $x_1 = 0 $ cả. Do đó $x_1$ không phải là cực trị, mặc dù khi đi qua $x_1$ thì $f'\left( x \right) $ có đổi dấu. Tuy nhiên ta luôn luôn chọn được một khoảng đủ nhỏ nằm trong đoạn $\left[ {0;4} \right]$ và chứa $x_2 = 2$, cùng với sự kiện $f'\left( x \right) $ đổi dấu từ âm sang dương khi đi qua $x_2$ nên đây là điểm cực tiểu, giá trị cực tiểu tương ứng là $f\left( {{x_2}} \right) = f\left( 2 \right) = - 3.$
Vậy hàm số có một cực tiểu và không có cực đại trên đoạn $\left[ {0;4} \right]$.
Bình luận. Nếu như ở ví dụ này ta xét trên $D$ thì rõ ràng $x_1$ là điểm cực đại. x = 0 \hfill \\
x = 2 \hfill \\
\end{gathered} \right..$$
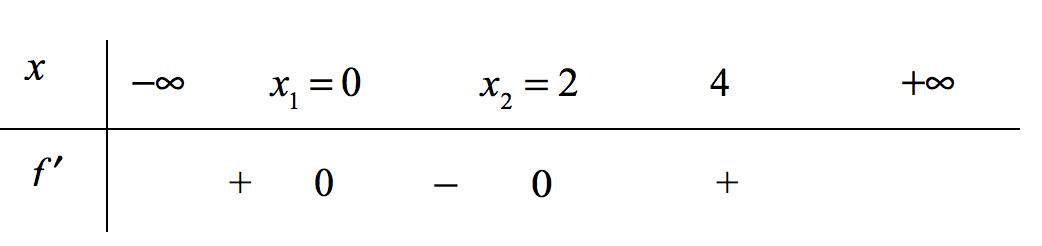
Trên đoạn $\left[ {0;4} \right]$ không tồn tại một khoảng nào chứa $x_1 = 0 $ cả. Do đó $x_1$ không phải là cực trị, mặc dù khi đi qua $x_1$ thì $f'\left( x \right) $ có đổi dấu. Tuy nhiên ta luôn luôn chọn được một khoảng đủ nhỏ nằm trong đoạn $\left[ {0;4} \right]$ và chứa $x_2 = 2$, cùng với sự kiện $f'\left( x \right) $ đổi dấu từ âm sang dương khi đi qua $x_2$ nên đây là điểm cực tiểu, giá trị cực tiểu tương ứng là $f\left( {{x_2}} \right) = f\left( 2 \right) = - 3.$
Vậy hàm số có một cực tiểu và không có cực đại trên đoạn $\left[ {0;4} \right]$.
Bài tập
Tác giả bài viết: Cùng Học Toán
Góp ý hoặc một bài toán của Quý học viên hoặc Quý Phụ Huynh