Tỷ mỷ làm toán. Độc lập suy nghĩ.
Tỷ mỷ làm toán. Độc lập suy nghĩ.
Công thức cung - góc liên kết
Hai góc đối nhau. Hai góc phụ nhau. Hai góc bù nhau. Sai góc hơn kém pi. Hai góc hơn kém pi/2.
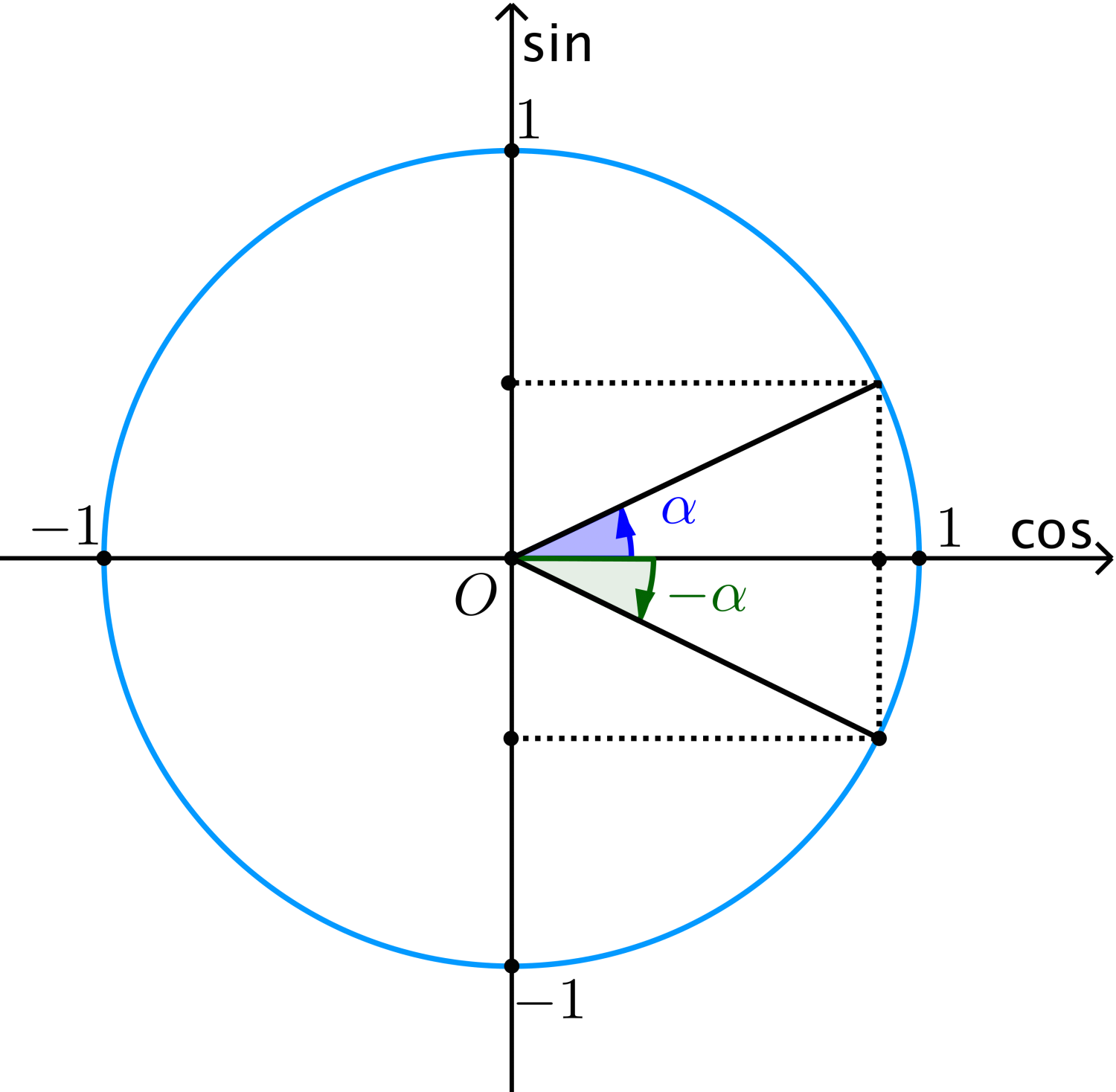
Công thức lượng giác - hai góc đối nhau. $\alpha $ và $-\alpha $
$$\eqalign{
& n\left( { - \alpha } \right) = - \sin \left( \alpha \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\cos \left( { - \alpha } \right) = \cos \alpha \cr
& \tan \left( { - \alpha } \right) = - \tan \left( \alpha \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\cot \left( { - \alpha } \right) = - \cot \left( \alpha \right) \cr} $$
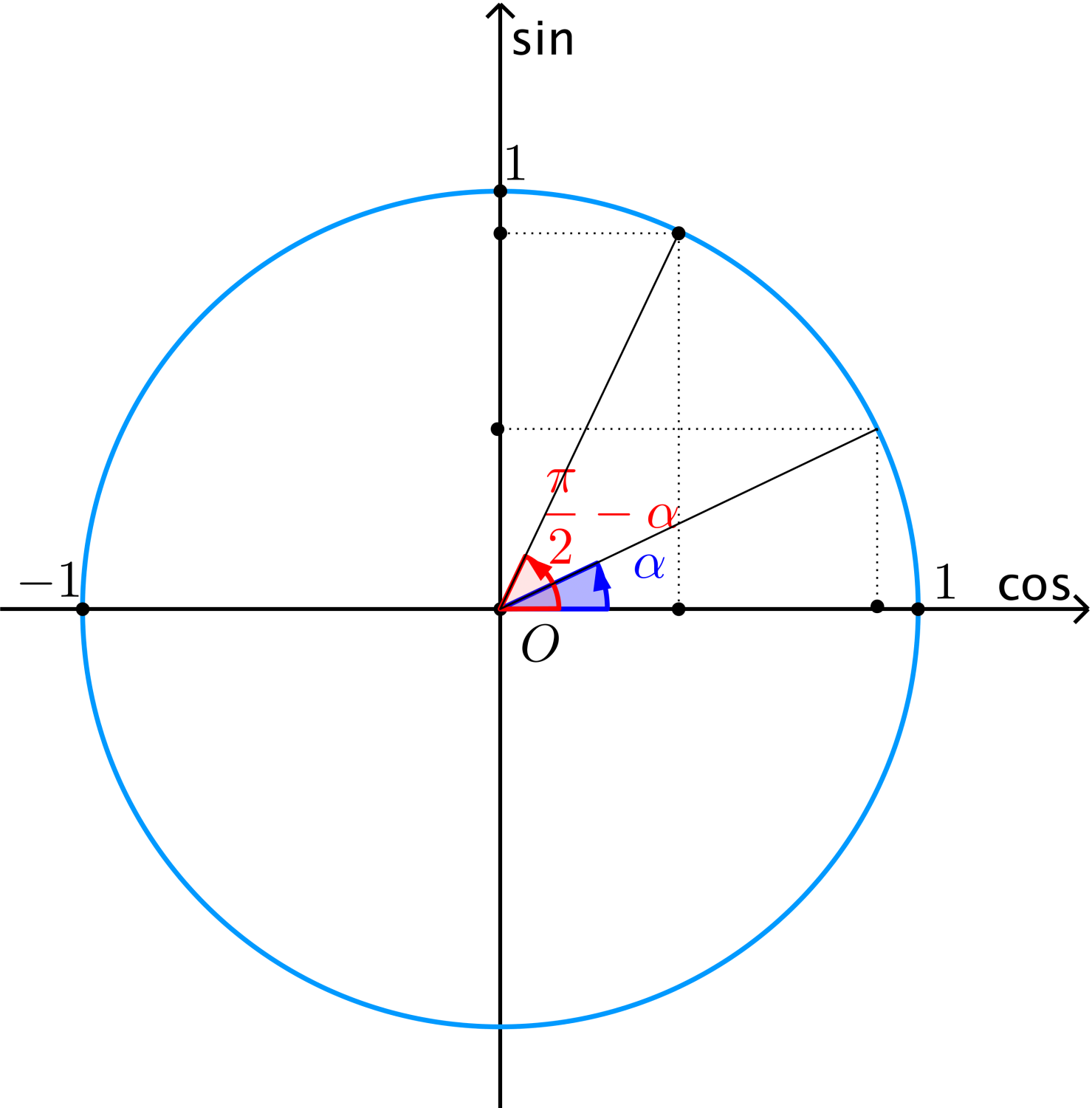
Công thức lượng giác - hai góc phụ nhau. $\alpha$ và $\frac{\pi }{2} - \alpha $.
$$\eqalign{
& \sin \left( {\frac{\pi }{2} - \alpha } \right) = \cos \alpha \;\;\;\;\;\;\;\;\;\;\;\;\;\cos \left( {\frac{\pi }{2} - \alpha } \right) = \sin \alpha \cr
& \tan \left( {\frac{\pi }{2} - \alpha } \right) = \cot \alpha \;\;\;\;\;\;\;\;\;\;\;\;\;\cot \left( {\frac{\pi }{2} - \alpha } \right) = \tan \alpha \cr} $$
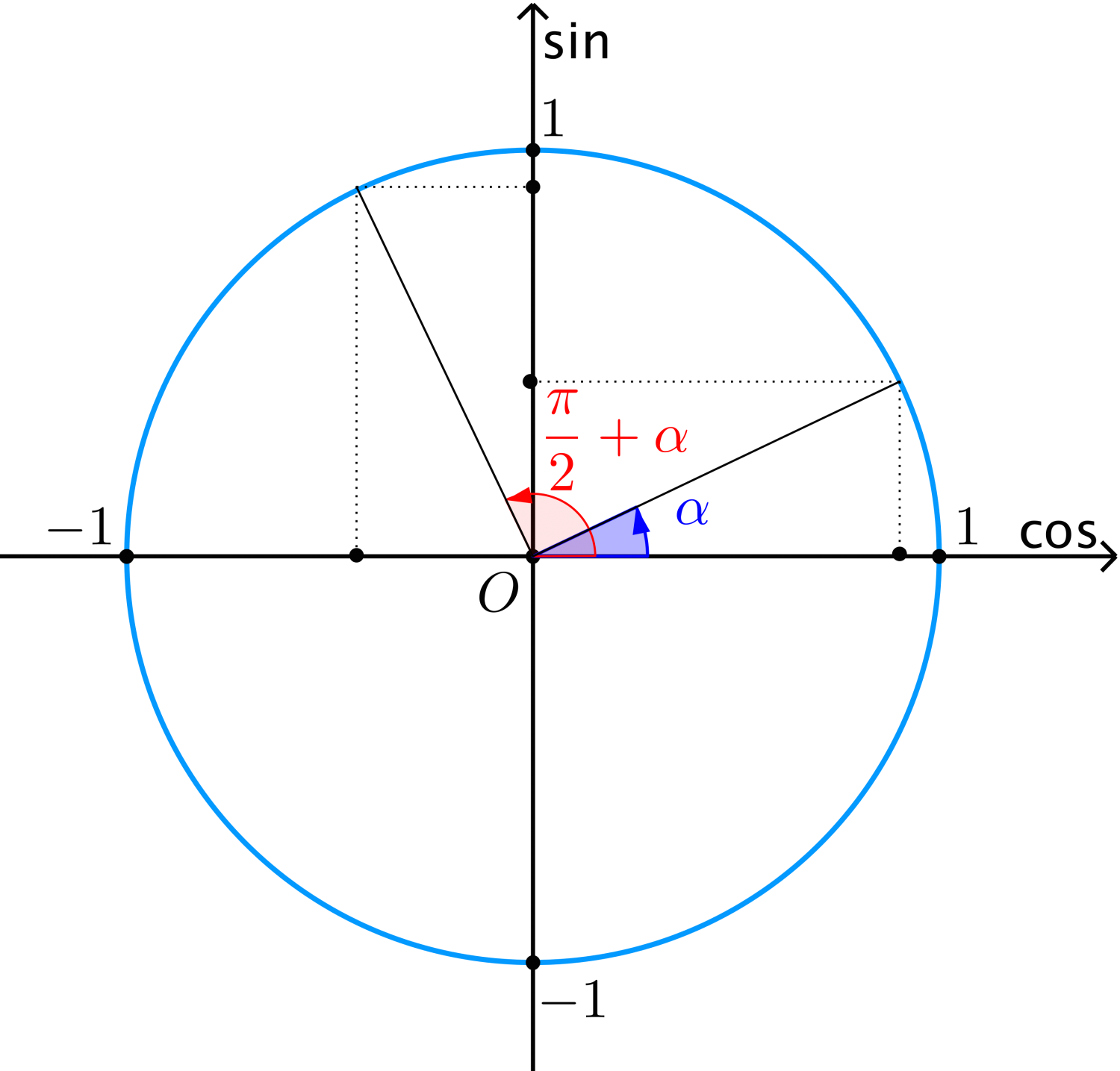
$$\eqalign{
& \sin \left( {\frac{\pi }{2} + \alpha } \right) = \cos \alpha \;\;\;\;\;\;\;\;\;\;\;\;\;\cos \left( {\frac{\pi }{2} + \alpha } \right) = - \sin \alpha \cr
& \tan \left( {\frac{\pi }{2} + \alpha } \right) = - \cot \alpha \;\;\;\;\;\;\;\;\;\;\cot \left( {\frac{\pi }{2} + \alpha } \right) = - \tan \alpha \cr} $$
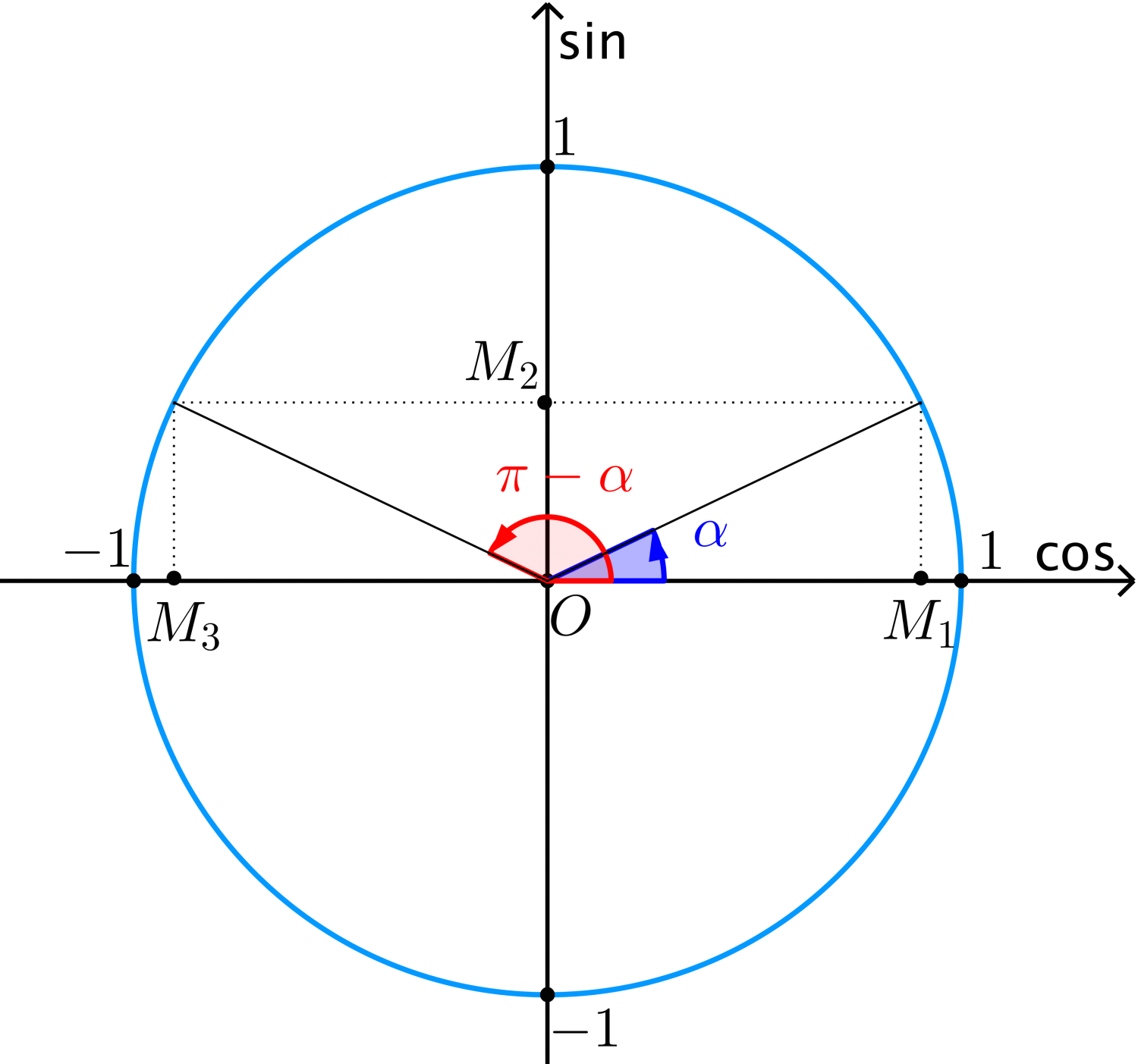
Công thức lượng giác - hai góc bù nhau. $\alpha$ và $\pi - \alpha $.
$$\eqalign{
& \sin \left( {\frac{\pi }{2} - \alpha } \right) = \cos \alpha \;\;\;\;\;\;\;\;\;\;\;\;\;\cos \left( {\frac{\pi }{2} - \alpha } \right) = \sin \alpha \cr
& \tan \left( {\frac{\pi }{2} - \alpha } \right) = \cot \alpha \;\;\;\;\;\;\;\;\;\;\;\;\;\cot \left( {\frac{\pi }{2} - \alpha } \right) = \tan \alpha \cr} $$
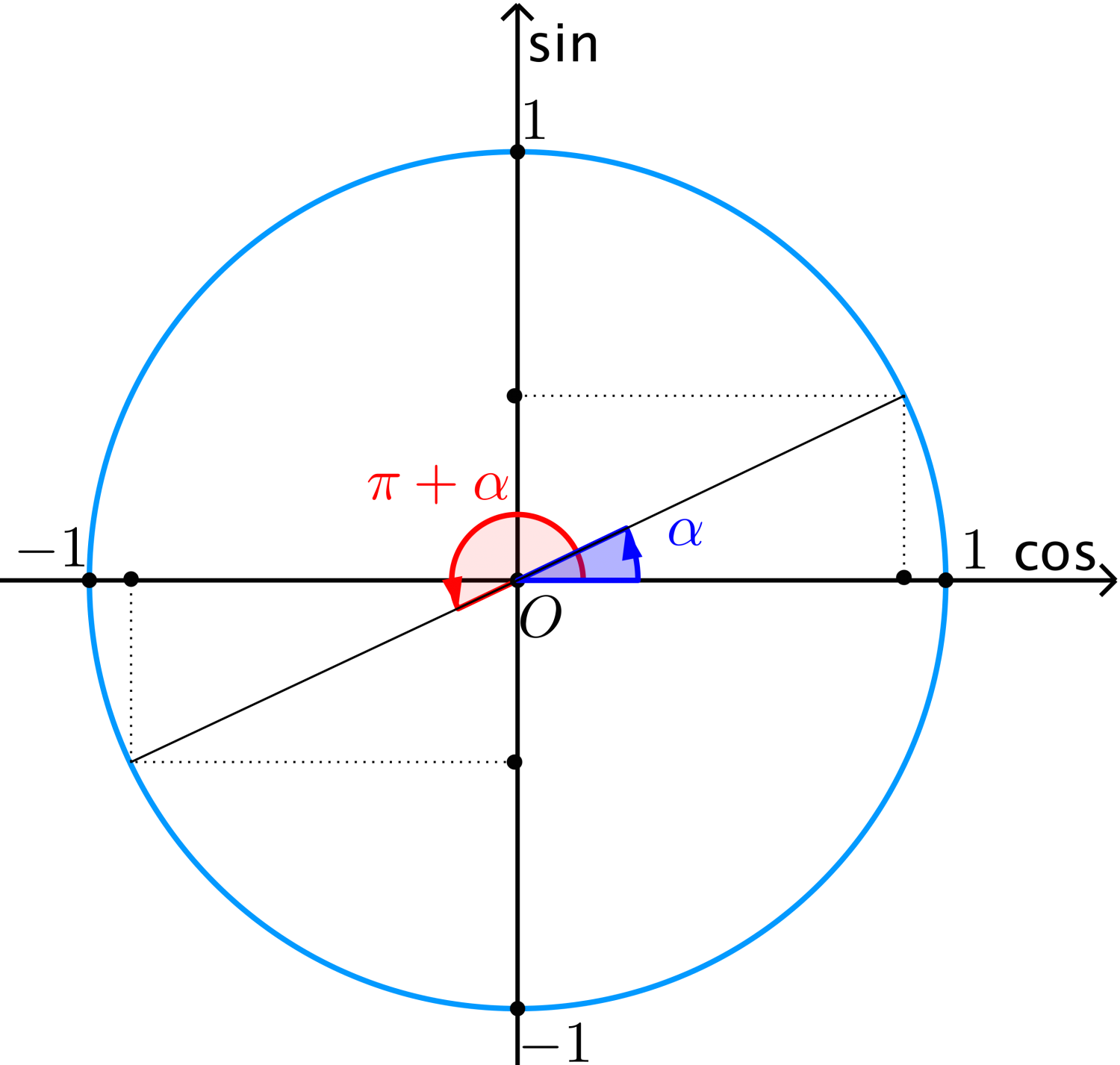
Công thức lượng giác - hai cung hơn kém nhau $\pi$. $\alpha$ và $\pi + \alpha $.
$$\eqalign{
& \sin \left( {\pi + \alpha } \right) = - \sin \alpha \;\;\;\;\;\;\;\;\;\;\;\cos \left( {\pi + \alpha } \right) = - \cos \alpha \cr
& \tan \left( {\pi + \alpha } \right) = \tan \alpha \;\;\;\;\;\;\;\;\;\;\;\;\;\cot \left( {\pi + \alpha } \right) = \cot \alpha \cr} $$
& \sin \left( {\pi + \alpha } \right) = - \sin \alpha \;\;\;\;\;\;\;\;\;\;\;\cos \left( {\pi + \alpha } \right) = - \cos \alpha \cr
& \tan \left( {\pi + \alpha } \right) = \tan \alpha \;\;\;\;\;\;\;\;\;\;\;\;\;\cot \left( {\pi + \alpha } \right) = \cot \alpha \cr} $$
Bài tập
(nhiều bài tập hơn khi đăng ký học tại Trung tâm Cùng học toán)
Tác giả bài viết: Cùng Học Toán
Góp ý hoặc một bài toán của Quý học viên hoặc Quý Phụ Huynh