Tỷ mỷ làm toán. Độc lập suy nghĩ.
Tỷ mỷ làm toán. Độc lập suy nghĩ.
Phương trình lượng giác cơ bản
Các phương trình lượng giác cơ bản
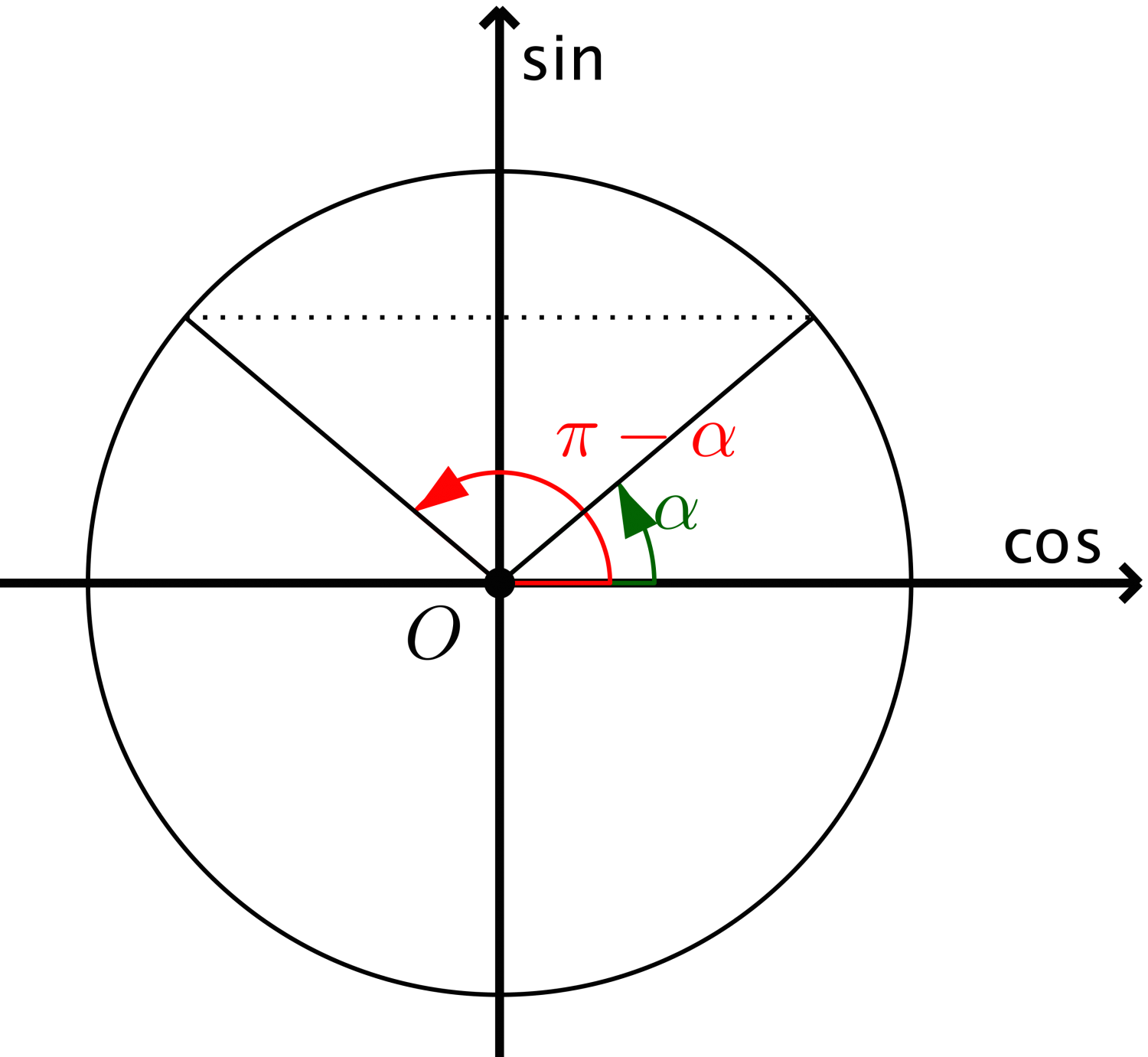
$$\sin x = \sin \alpha \Leftrightarrow \left[ \begin{gathered}
x = \alpha + k2\pi \hfill \\
x = \pi - \alpha + k2\pi \hfill \\
\end{gathered} \right.,k \in \mathbb{Z}.$$
Ví dụ 1. $\sin x = \frac{1}{2} \Leftrightarrow \sin x = \sin \frac{\pi }{6} \Leftrightarrow \left[ \begin{gathered}
x = \frac{\pi }{6} + k2\pi \hfill \\
x = \frac{{5\pi }}{6} + k2\pi \hfill \\
\end{gathered} \right.$
Ví dụ 2. Giải phương trình $\sin x = \frac{1}{3}{\text{ }}\left( * \right)$.
Đặt $\alpha = \arcsin \left( {\frac{1}{3}} \right),$ tức là $\sin \alpha = \frac{1}{3}.$
$$\left( * \right) \Leftrightarrow \sin x = \sin \alpha \Leftrightarrow \left[ \begin{gathered}
x = \alpha + k2\pi \hfill \\
x = \pi - \alpha + k2\pi \hfill \\
\end{gathered} \right..$$
$$\left( * \right) \Leftrightarrow \sin x = \sin \alpha \Leftrightarrow \left[ \begin{gathered}
x = \alpha + k2\pi \hfill \\
x = \pi - \alpha + k2\pi \hfill \\
\end{gathered} \right..$$
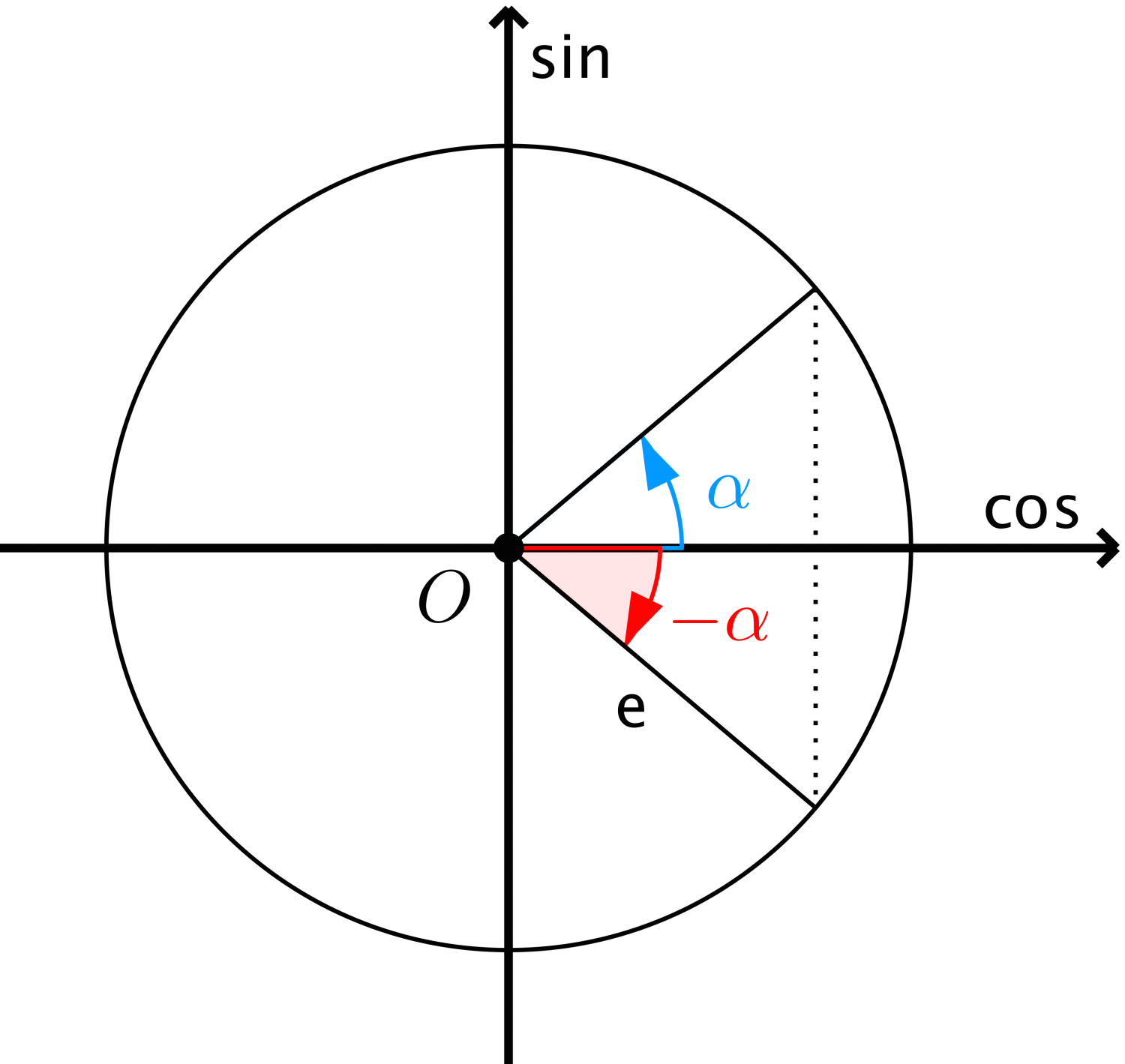
$$\cos x = \cos \alpha \Leftrightarrow \left[ \begin{gathered}
x = \alpha + k2\pi \hfill \\
x = - \alpha + k2\pi \hfill \\
\end{gathered} \right.$$
Ví dụ 3. $\cos x = \frac{1}{2} \Leftrightarrow \cos x = \cos \frac{\pi }{3} \Leftrightarrow \left[ \begin{gathered}
x = \frac{\pi }{3} + k2\pi \hfill \\
x = - \frac{\pi }{3} + k2\pi \hfill \\
\end{gathered} \right..$
Ví dụ 4. $\cos x = \frac{1}{3}{\text{ }}\left( * \right)$. Đặt $\alpha = \arccos \left( {\frac{1}{3}} \right),$ tức là $\cos \alpha = \frac{1}{3}.$
$$\left( * \right) \Leftrightarrow \sin x = \sin \alpha \Leftrightarrow \left[ \begin{gathered}
x = \alpha + k2\pi \hfill \\
x = - \alpha + k2\pi \hfill \\
\end{gathered} \right..$$
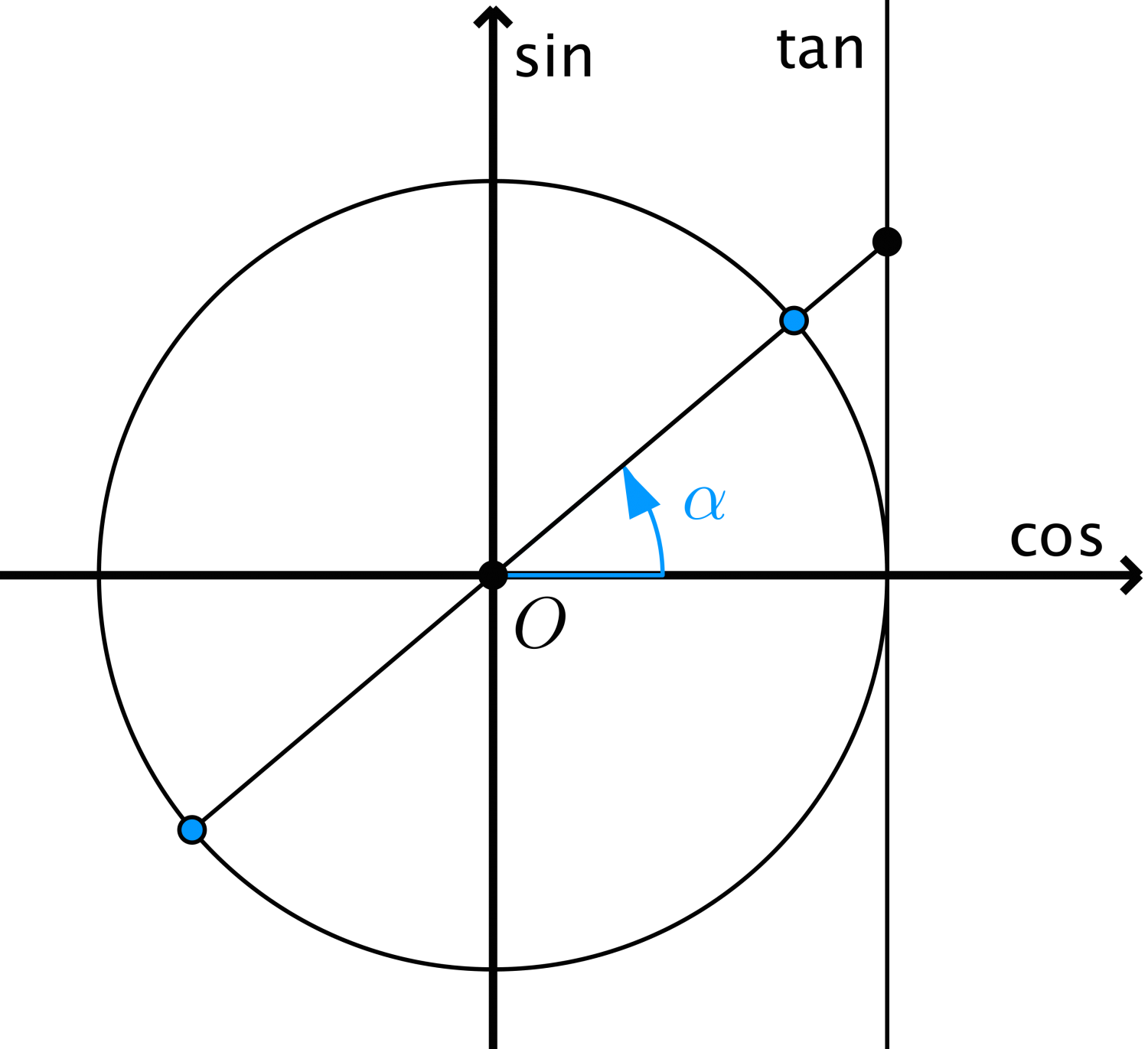
$$\tan x = \tan \alpha \Leftrightarrow x = k\pi .$$
Ví dụ 5. $\tan x = \tan \alpha \Leftrightarrow x = k\pi .$
Ví dụ 6. Giải phương trình $\tan x = 3{\text{ }}\left( * \right)$ Đặt $\alpha = \arctan 3,$ tức là $\tan \alpha = 3.$
$$\left( * \right) \Leftrightarrow \tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi .$$
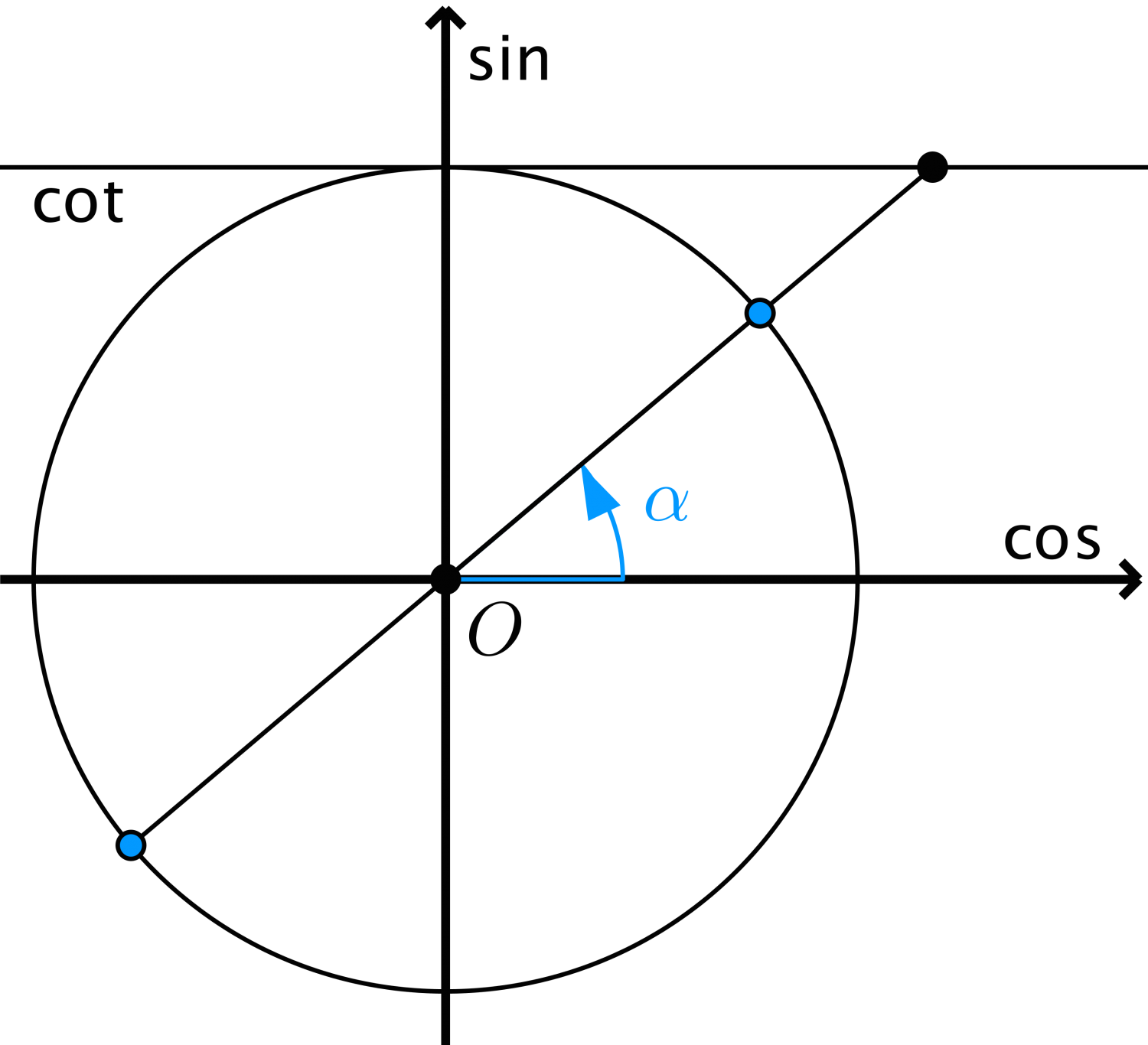
$$\cot x = \cot \alpha \Leftrightarrow x = k\pi .$$
Ví dụ 7. $\cot x = \frac{1}{{\sqrt 3 }} \Leftrightarrow \cot x = \cot \frac{\pi }{3} \Leftrightarrow x = \frac{\pi }{3} + k\pi .$
Ví dụ 8. Giải phương trình $\cot x = 3{\text{ }}\left( * \right)$. Đặt $\alpha = \operatorname{arc} \cot 3,$ tức là $\cot \alpha = 3.$
$$\left( * \right) \Leftrightarrow \cot x = \cot \alpha \Leftrightarrow x = \alpha + k\pi .$$
Bài tập
(nhiều bài tập hơn khi đăng ký học tại Trung tâm Cùng học toán)
Tác giả bài viết: Cùng Học Toán
Góp ý hoặc một bài toán của Quý học viên hoặc Quý Phụ Huynh