Biện luận số nghiệm của phương trình bằng đồ thị
- Thứ ba - 21/06/2016 02:45
- In ra
- Đóng cửa sổ này
Biện luận số nghiệm của phương trình bằng đồ thị.
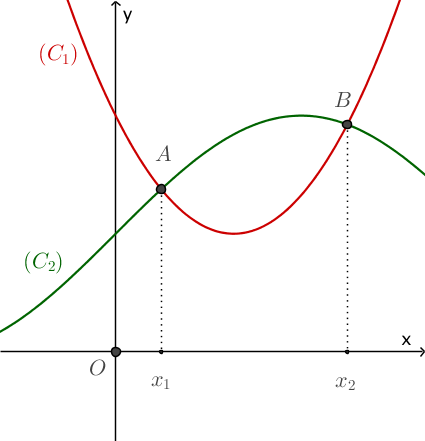
Chẳng hạn như hình bên, hai đường cong $\left( {{C_1}} \right)$ và $\left( {{C_2}} \right)$ cắt nhau tại hai điểm phân biệt $A$ và $B$ nên phương trình $f\left( x \right) = g\left( x \right)$ có hai nghiệm phân biệt, và nghiệm của phương trình này chính là $x_1$ và $x_2$, lần lượt là hoành độ của $A$ và $B$.
Bài toán Biện luận số nghiệm của phương trình bằng đồ thị thường rơi vào các dạng sau đây:
Biện luận theo tham số $m$ số nghiệm của phương trình dạng $f\left( x \right) = g\left( m \right).$
Bước 1. Vẽ đồ thị 
$\left( C \right)$ của hàm số 
$y = f\left( x \right)$; và đường thẳng 
$\Delta :y = g\left( m \right)$ là đường thẳng song song với 
$Ox$ và cắt $Oy$
tại điểm có tung độ là $g\left( m \right).$ 
Bước 2. Kết luận số nghiệm của 
$\left( 1 \right):$ số nghiệm của 
$\left( 1 \right)$ là số giao điểm của 
$\left( C \right)$ và $\Delta .$
Ví dụ 1. Biện luận số nghiệm của phương trình ${x^3} - 6{x^2} + 9x + 1 - m = 0$ bằng đồ thị.
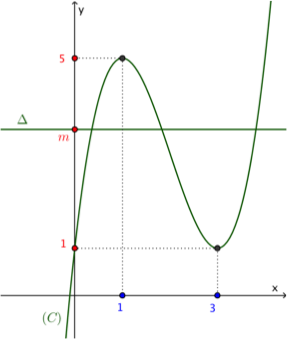
Khi $m$ thay đổi thì đường thẳng $\Delta$ sẽ dịch chuyển lên-xuống, luôn song song với $Ox$. Do đó ta có
$\bullet$ $1 < m < 5$ thì $\Delta $ cắt $\left( C \right)$ tại ba điểm phân biệt nên $\left( 1 \right)$ có ba nghiệm phân biệt.
$\bullet$ $m=1$ hoặc $m=5$ thì $\Delta $ cắt $\left( C \right)$ tại hai điểm phân biệt nên $\left( 1 \right)$ có hai nghiệm phân biệt.
$\bullet$ $m<1$ hoặc $m>5$ thì $\Delta $ cắt $\left( C \right)$ tại một điểm duy nhất nên $\left( 1 \right)$ có một nghiệm duy nhất.
Bình luận 1. Khi $m = 1$ thì đường thẳng $\Delta $ vừa tiếp xúc, vừa cắt $\left( C \right).$ Trong trường hợp này $\left( 1 \right)$ có hai nghiệm, trong đó có một nghiệm kép và một nghiệm đơn. Nghiệm kép bi