Phép đối xứng tâm

Phép đối xứng tâm. Cho điểm $I$. Phép biến hình biến điểm $I$ thành chính nó, biến mỗi điểm $M$ khác $I$ thành điểm $M'$ sao cho $I$ là trung điểm của $MM'$ được gọi là phép đối xứng tâm $I$.

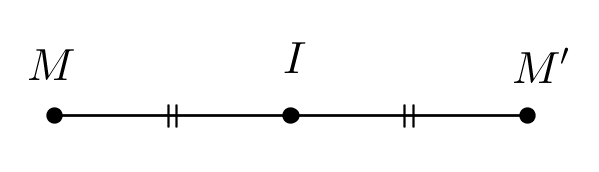
Phép đối xứng tâm $I$ ký hiệu là ${D_I}.$ 

Ta viết ${D_I}\left( M \right) = M'$ để chỉ phép đối xứng tâm $I$ biến điểm $M$ thành điểm $M'$. 

Từ định nghĩa ta dễ dàng suy ra ${D_I}\left( M \right) = M' \Leftrightarrow \overrightarrow {IM'}  =  - \overrightarrow {IM} .$

Các tính chất của phép đối xứng tâm. Phép đối xứng tâm bảo toàn khoảng cách giữa hai điểm bất kì, biến đường thẳng thành đường thẳng, biến tam giác thành tam giác đã cho, biến đường tròn thành đường tròn có cùng bán kính.


 

Đối xứng qua gốc toạ độ. Trong mặt phẳng $Oxy$ cho điểm $M\left( {x;y} \right).$ Khi đó phép cho ảnh qua phép đối xứng tâm $O\left( {0;0} \right)$ là $${D_O}\left( M \right) = M'\left( { - x; - y} \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left(  *  \right)$$

Bình luận 1. Trong mặt phẳng $Oxy$, để tìm ảnh của một điểm qua một phép đối xứng tâm $O$, thì theo theo công thức $(*)$, ta chỉ cần đổi dấu của các toạ độ của điểm đó. 

Ví dụ 1. Trong mặt phẳng $Oxy$, ảnh của điểm $A\left( {1; - 2} \right)$ qua phép đối xứng tâm $D_O$, với $O$ là gốc toạ độ, là $A'\left( { - 1;2} \right)$.

Ví dụ 2. Trong mặt phẳng $Oxy$, tìm phương trình đường thẳng $\Delta '$ là ảnh của đường thẳng $\Delta :2x + 3y - 1 = 0$ qua phép đối xứng tâm $D_O$.