Bài toán thiết diện: song song với một đường.
- Thứ năm - 25/02/2016 15:54
- In ra
- Đóng cửa sổ này
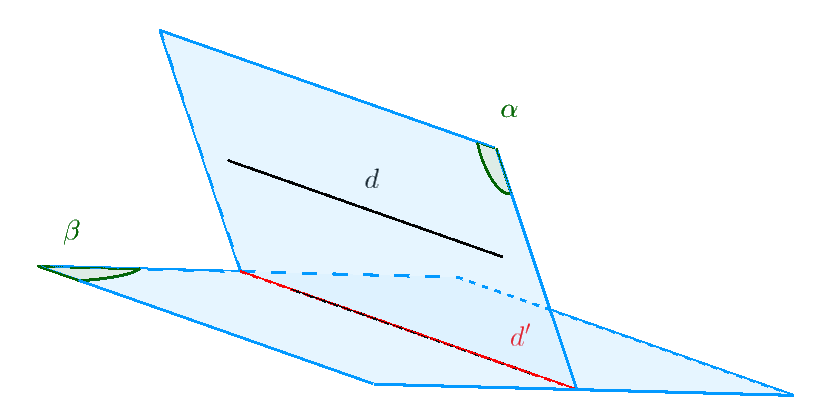
Bài toán xác định thiết diện song song với đường thẳng.
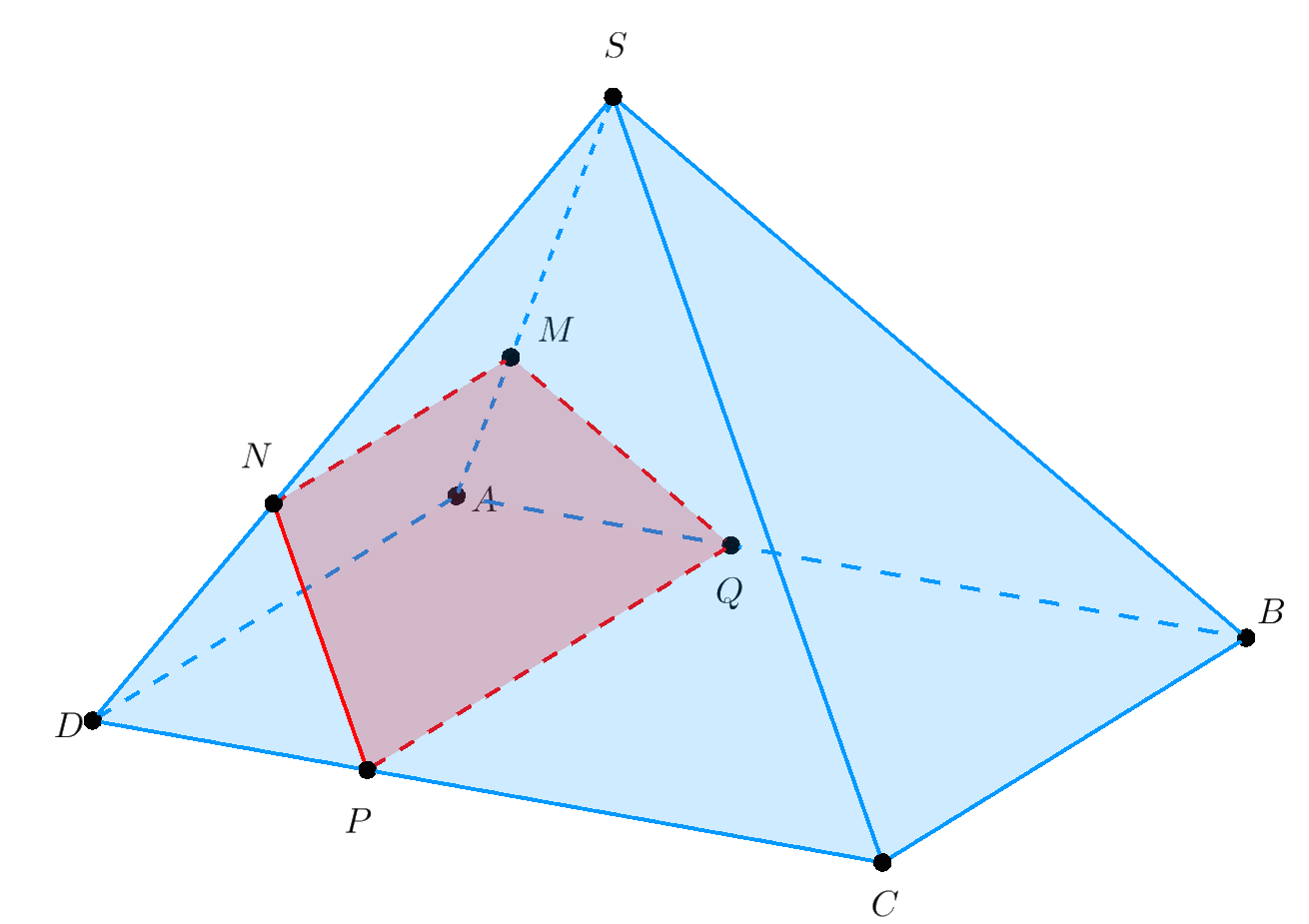
Giải. Vì $\left( \alpha \right)//AD \subset \left( {SAD} \right) \Rightarrow \left( \alpha \right) \cap \left( {SAD} \right) = MN//AD,N \in SD.$
Tương tự do $\left( \alpha \right)//SC \subset \left( {SCD} \right)$
$ \Rightarrow \left( \alpha \right) \cap \left( {SCD} \right) = NP//SC,P \in CD.$
Mặt khác $\left( \alpha \right)//AD \subset \left( {ABCD} \right)$ $ \Rightarrow \left( \alpha \right) \cap \left( {ABCD} \right) = PQ//AD,Q \in AB.$
Khi đó $\left( \alpha \right) \cap \left( {SAB} \right) = MQ.$
Vậy $MNPQ$ là thiết diện cần tìm.