Đạo hàm
- Thứ sáu - 12/02/2016 20:07
- In ra
- Đóng cửa sổ này
Định nghia đạo hàm hàm. Đạo hàm của một số hàm số cơ bản.
| Đạo hàm. Cho hàm số $f\left( x \right)$ xác định trên khoảng $\left( {a;b} \right)$ chứa ${x_0}.$ Giới hạn hữu hạn $\hbox{(nếu có)}$ $$\mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}$$ được gọi là đạo hàm của hàm số $f\left( x \right)$ tại ${x_0}.$ Ký hiệu $f'\left( {{x_0}} \right).$ |
Ví dụ 1. Tính đạo hàm của hàm số $f\left( x \right) = {x^2} + 1$ tại ${x_0} = 2.$
Giải. $$f'\left( 2 \right) = \mathop {\lim }\limits_{x \to 2} \frac{{f\left( x \right) - f\left( 2 \right)}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{{x^2} + 1 - 5}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{{x^2} - 4}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \left( {x + 2} \right) = 4.$$
| Đạo hàm. Hàm số $f\left( x \right)$ được gọi là có đạo hàm trên khoảng $\left( {a;b} \right)$ nếu $f\left( x \right)$ có đạo hàm tại mọi điểm $x_0$ thuộc khoảng $\left( {a;b} \right)$. Nếu hàm số $f\left( x \right)$ có đạo hàm trên khoảng $\left( {a;b} \right)$ thì hàm số $f'\left( x \right)$ xác định tại mọi $x \in \left( {a;b} \right)$ được gọi là đạo hàm của hàm số $f\left( x \right)$ trên khoảng $\left( {a;b} \right)$. |
Ví dụ 2. Tìm đạo hàm của hàm số $f\left( x \right) = {x^3} $ trên tập xác định $\mathbb{R}$.
Giải. Với mọi ${x_0} \in \mathbb{R}$ ta có
$$\mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{{x^3} - x_0^3}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{\left( {x - {x_0}} \right)\left( {{x^2} + x{x_0} + x_0^2} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \left( {{x^2} + x{x_0} + x_0^2} \right) = 3x_0^2.$$ Vậy $f'\left( x \right) = 3{x^2}.$
$$\mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{{x^3} - x_0^3}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{\left( {x - {x_0}} \right)\left( {{x^2} + x{x_0} + x_0^2} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \left( {{x^2} + x{x_0} + x_0^2} \right) = 3x_0^2.$$ Vậy $f'\left( x \right) = 3{x^2}.$
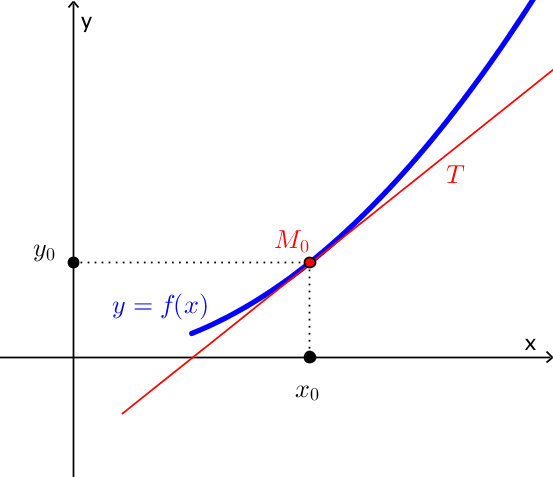
Ý nghĩa của đạo hàm. Giá trị $f'\left( {{x_0}} \right)$ là hệ số góc của tiếp tuyến của đồ thị hàm số $f\left( x \right)$ tại $x_0$.
Từ đây ta có, phương trình tiếp tuyến $T$ của hàm số $y=f\left( x \right)$ tại điểm có hoành độ $x_0$ là
$$y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + {y_0}.\;\;$$
Dưới đây là đạo hàm của các hàm số cơ bản. Ta sẽ không chứng minh các công thức này mà chú trọng vào cách dùng.
| Đạo hàm của các hàm số cơ bản. $$\begin{array}{l} \left( 1 \right)\;\;\;\;\;C' = 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( 2 \right)\;\;\;\;\;{\left( x \right)^\prime } = 1.\\ \left( 3 \right)\;\;\;\;\;{\left( {{x^n}} \right)^\prime } = n{x^{n - 1}},n \in N.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( 4 \right)\;\;\;\;{\left( {\frac{1}{x}} \right)^\prime } = - \frac{1}{{{x^2}}}.\\ \left( 5 \right)\;\;\;\;\;{\left( {\sqrt x } \right)^\prime } = \frac{1}{{2\sqrt x }}.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( 6 \right)\;\;\;\;{\left( {\sin x} \right)^\prime } = \cos x.\\ \left( 7 \right)\;\;\;\;\;{\left( {\cos x} \right)^\prime } = - \sin x.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( 8 \right)\;\;\;\;{\left( {\tan x} \right)^\prime } = \frac{1}{{{{\cos }^2}x}} = 1 + {\tan ^2}x.\\ \left( 9 \right)\;\;\;\;\;{\left( {\cot x} \right)^\prime } = - \frac{1}{{{{\sin }^2}x}} = - \left( {1 + {{\cot }^2}x} \right).\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \end{array}$$ |
| Các quy tắc tính đạo hàm. Với $C$ là hằng số, $u\left( x \right)$ và $v\left( x \right)$ là các hàm số ta có $$\begin{array}{l} \left( a \right)\;\;\;\;\;\;\;{\left( {u + v} \right)^\prime } = u' + v'.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( b \right)\;\;\;\;\;\;\;{\left( {u - v} \right)^\prime } = u' - v'.\\ \left( b \right)\;\;\;\;\;\;\;{\left( {C \cdot u} \right)^\prime } = C \cdot u'\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {b'} \right)\;\;\;\;\;\;\;{\left( {u \cdot v} \right)^\prime } = u' \cdot v + v' \cdot u.\\ \left( c \right)\;\;\;\;\;\;{\left( {\frac{1}{v}} \right)^\prime } = - \frac{{v'}}{{{v^2}}}.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {c'} \right)\;\;\;\;\;\;\;{\left( {\frac{u}{v}} \right)^\prime } = \frac{{u' \cdot v - v' \cdot u}}{{{v^2}}}. \end{array}$$ |
Ví dụ 4. $$\begin{array}{l}
f\left( x \right) = 2{x^3} - 5{x^2} + 3x + 2 \Rightarrow f'\left( x \right) = {\left( {2{x^3}} \right)^\prime } - {\left( {5{x^2}} \right)^\prime } + {\left( {3x} \right)^\prime } + 2'\\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = 2{\left( {{x^3}} \right)^\prime } - 5{\left( {{x^2}} \right)^\prime } + 3{\left( x \right)^\prime } + 2' = 6{x^2} - 10x + 3.
\end{array}$$
Ví dụ 5. Áp dụng quy tắc $\left( {c'} \right)$ ta có $$\begin{array}{l}
f\left( x \right) = \frac{{{x^2} + 1}}{{{x^3} - 2x + 1}} \Rightarrow f'\left( x \right) = \frac{{{{\left( {{x^2} + 1} \right)}^\prime }\left( {{x^3} - 2x + 1} \right) - {{\left( {{x^3} - 2x + 1} \right)}^\prime }\left( {{x^2} + 1} \right)}}{{{{\left( {{x^3} - 2x + 1} \right)}^2}}}\\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{{2x\left( {{x^3} - 2x + 1} \right) - \left( {3{x^2} - 2} \right)\left( {{x^2} + 1} \right)}}{{{{\left( {{x^3} - 2x + 1} \right)}^2}}} = \frac{{ - {x^4} - 5{x^2} + 2x + 2}}{{{{\left( {{x^3} - 2x + 1} \right)}^2}}}.
\end{array}$$
Ví dụ 6. Viết phương trình tiếp tuyến của đồ thị hàm số $f\left( x \right) = \sin x$ tại ${x_0} = \frac{\pi }{6}$.
Giải. Với ${x_0} = \frac{\pi }{6} \Rightarrow {y_0} = f\left( {{x_0}} \right) = \sin \frac{\pi }{6} = \frac{1}{2}.$
Áp dụng công thức $\left( 6 \right)$ ta có $$f'\left( x \right) = \cos x \Rightarrow f'\left( {{x_0}} \right) = \cos \frac{\pi }{6} = \frac{{\sqrt 3 }}{2}.$$ Phương trình tiếp tuyến $$y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + {y_0} \Leftrightarrow y = \frac{{\sqrt 3 }}{2}\left( {x - \frac{\pi }{6}} \right) + \frac{1}{2} \Leftrightarrow y = \frac{{\sqrt 3 }}{2}x + \frac{1}{2} - \frac{{\sqrt 3 \pi }}{{12}}.$$
Áp dụng công thức $\left( 6 \right)$ ta có $$f'\left( x \right) = \cos x \Rightarrow f'\left( {{x_0}} \right) = \cos \frac{\pi }{6} = \frac{{\sqrt 3 }}{2}.$$ Phương trình tiếp tuyến $$y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + {y_0} \Leftrightarrow y = \frac{{\sqrt 3 }}{2}\left( {x - \frac{\pi }{6}} \right) + \frac{1}{2} \Leftrightarrow y = \frac{{\sqrt 3 }}{2}x + \frac{1}{2} - \frac{{\sqrt 3 \pi }}{{12}}.$$