Sự biểu diễn của số phức
- Thứ ba - 05/04/2016 17:14
- In ra
- Đóng cửa sổ này
Mặt phẳng phức. Dạng lượng giác của số phức. Căn và luỹ thừa của số phức.
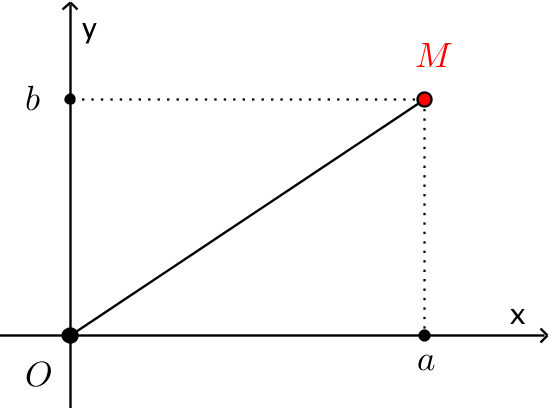
Sự biểu diễn của số phức. Mặt phẳng phức. Mỗi số phức $z = a + bi,$ với $ a,b \in \mathbb{R} $ được biểu diễn bởi duy nhất một điểm $M\left( {a;b} \right)$ trong mặt phẳng toạ độ $Oxy$. Cùng với sự biểu diễn này thì mặt phẳng $Oxy$ được gọi là mặt phẳng phức.
Trục hoành $Ox$ biễu diễn cho thành phần thực của $z$ nên được gọi là trục thực, trục tung $Oy$ biểu diễn cho thành phần ảo, được gọi là trục ảo.
Bình luận 1. Từ đây ta cũng suy ra số phức $z = a + bi$ và liên hợp của nó là $z = a - bi$ được biểu diễn bởi hai điểm đối xứng nhau qua trục hoành; số phức $z = a + bi$ và số phức đối của nó là $-z = -a - bi$ được biểu diễn bởi hai điểm đối xứng qua gốc toạ độ. Học sinh hãy thử tự biểu diễn để kiểm chứng điều này.
Môđun của số phức. Đại lượng $\sqrt {{a^2} + {b^2}} $ được gọi là môđun của $z$, ký hiệu $\left| z \right|$, và đại lượng này cũng chính là độ dài của đoạn thẳng $OM$. Do đó, $\left| z \right|$ đôi khi còn được gọi là độ lớn của số phức $z$.
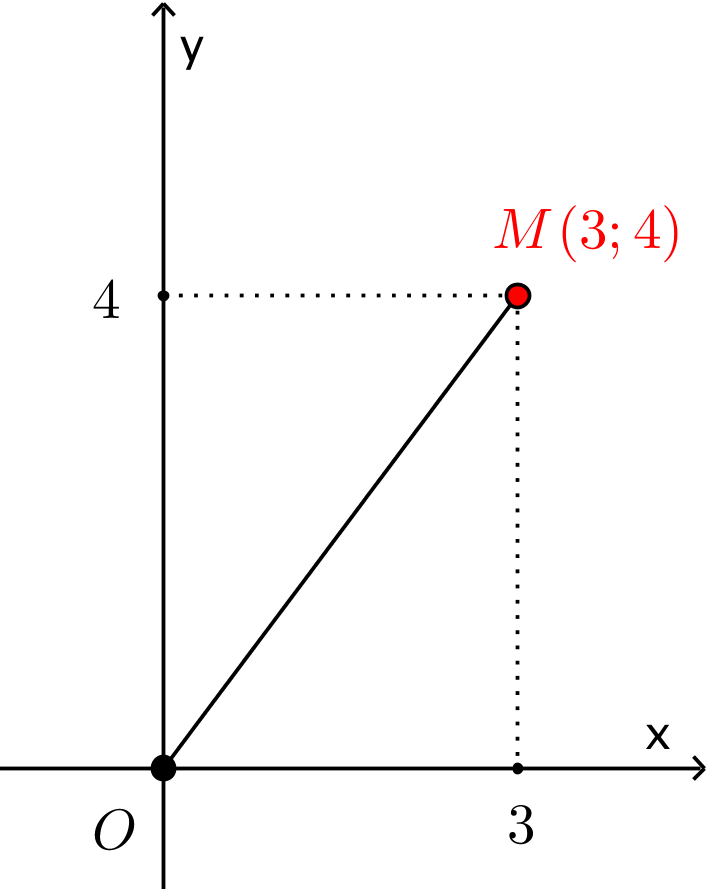
Ví dụ 1. Biễu diễn và tính mô-đun của số phức $z = 3 + 4i$.
Giải. Ta có $\left| z \right| = \sqrt {{a^2} + {b^2}} = \sqrt {{3^2} + {4^2}} = 5.$
Bằng định lý Pitago ta dễ dàng kiểm chứng $\left| z \right| = OM = 5.$
Bằng định lý Pitago ta dễ dàng kiểm chứng $\left| z \right| = OM = 5.$
Số phức được viết dưới dạng $z = a + bi$ còn được gọi là dạng đại số của số phức. Sau đây là cách biểu diễn khác của số phức $z = a + bi$.
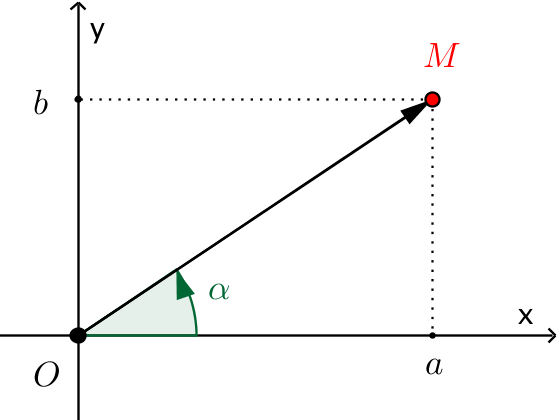
Dạng lượng giác của số phức. Gọi $\alpha$ là góc hợp bởi $\overrightarrow {OM} $ và chiều dương của trục $Ox$. Đặt $r = \left| z \right| = \sqrt {{a^2} + {b^2}} .$
Khi đó ta có $$\left\{ \begin{gathered} a = r\cos \alpha \hfill \\ b = r\sin \alpha \hfill \\ \end{gathered} \right..$$ Khi đó số phức $z$ được viết lại $$z = r\left( {\cos \alpha + i\sin \alpha } \right).$$ Góc $ \alpha $ được gọi là argument của số phức $ z $, ký hiệu $ \arg \left( z \right). $
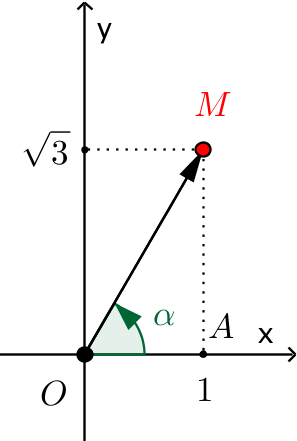
Sử dụng hệ thức lượng trong tam giác vuông $OAM$ ta có $$\tan \alpha = \frac{{OM}}{{OA}} = \frac{{\sqrt 3 }}{1} = \sqrt 3 \Rightarrow \alpha = {60^o}.$$ Mô đun của $ z $ là $$\left| z \right| = \sqrt {{1^2} + {{\sqrt 3 }^2}} = 2.$$ Từ đây ta có dạng lượng giác của $z$ là $$z = 2\left( {\cos {{60}^o} + i\sin {{60}^o}} \right).$$
Một cách biến đổi khác để được dạng lượng giác của $z$ là $$z = 1 + \sqrt 3 i = 2\left( {\frac{1}{2} + \frac{{\sqrt 3 }}{2}i} \right) = 2\left( {\cos {{60}^o} + i\sin {{60}^o}} \right).$$
