Phép quay
Phép quay. Tìm ảnh qua phép quay.
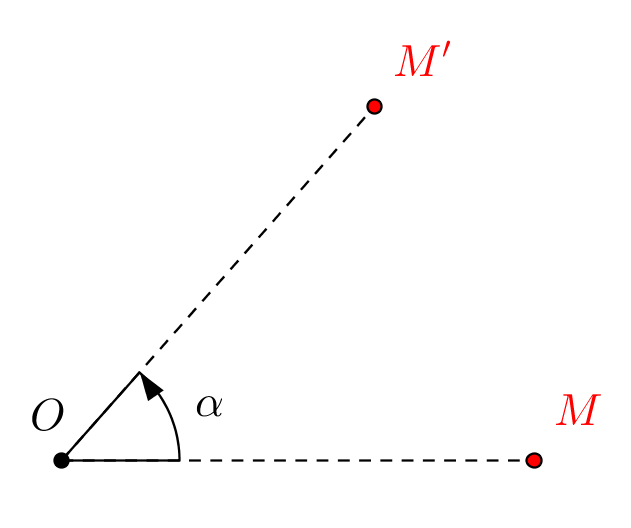
Điểm $O$ được gọi là tâm quay, $\alpha$ được gọi là góc quay.
Ta viết ${Q_{\left( {O,\alpha } \right)}}\left( M \right) = M'$ để chỉ phép quay ${Q_{\left( {O,\alpha } \right)}}$ biến điểm $M$ thành điểm $M'$.
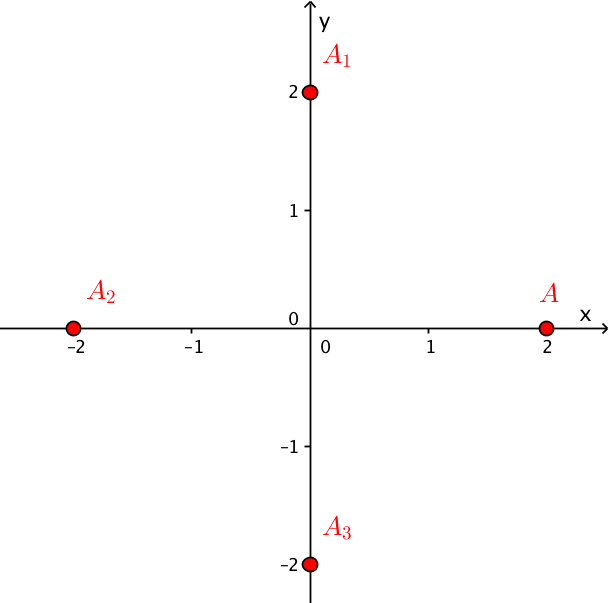
Ví dụ 1. Trong mặt phẳng $Oxy$, cho điểm $A\left( {2;0} \right)$.
Phép quay ${Q_{\left( {O,{{90}^0}} \right)}}$ biến điểm $A$ thành điểm ${A_1}\left( {0;2} \right)$.
Phép quay ${Q_{\left( {O,{{180}^0}} \right)}}$ biến điểm $A$ thành điểm ${A_2}\left( {0;-2} \right)$.
Phép quay ${Q_{\left( {O,{{-90}^0}} \right)}}$ biến điểm $A$ thành điểm ${A_3}\left( {-2;0} \right)$.
Phép quay ${Q_{\left( {O,{{360}^0}} \right)}}$ biến điểm $A$ thành chính nó.
Bình luận 1. Trong ví dụ trên, $A_3$ và $A$ đối xứng nhau qua gốc toạ độ $O$. Như vậy ${Q_{\left( {O,{{180}^0}} \right)}}$ trùng với phép đối xứng tâm $D_O$, còn phép quay ${Q_{\left( {O,{{360}^0}} \right)}}$ trùng với phép đồng nhất. Tổng quát hơn ta có
|
Trong mặt phẳng $Oxy$ ta luôn có
$(i)$ phép quay ${Q_{\left( {O,\left( {2k + 1} \right)\pi } \right)}}$ trùng với phép đối xứng tâm $D_O$,
$(ii)$ phép quay ${Q_{\left( {O,2k\pi } \right)}}$ trùng với phép đồng nhất,
với $k\in \mathbb{Z}$.
|
Các tính chất của phép quay. Phép quay bảo toàn khoảng cách giữa hai điểm bất kì, biến đường thẳng thành đường thẳng, biến tam giác thành tam giác đã cho, biến đường tròn thành đường tròn có cùng bán kính.
Ví dụ 2. Trong mặt phẳng $Oxy$ viết phương trình đường tròn $\left( {C'} \right)$ là ảnh của đường tròn $\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 4$ qua phép quay ${Q_{\left( {O,{{60}^0}} \right)}}$.
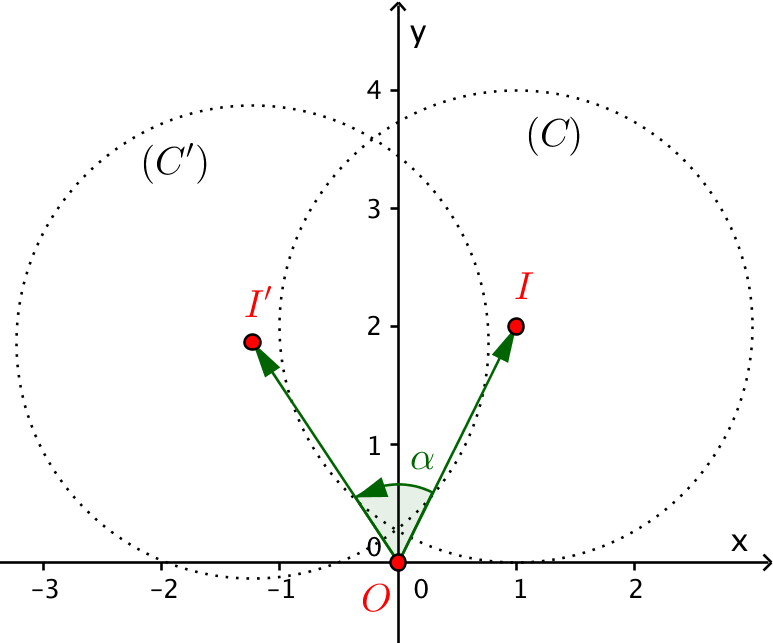
Giải. Tâm và bán kính của đường tròn $\left( C \right)$ lần lượt là $I\left( {1;2} \right)$ và $R=2$. Gọi $I'$ và $R'$ lần lượt là tâm và bán kính của đường tròn $\left( {C'} \right)$. Vì phép quay có tính chất bảo toàn độ dài đoạn thẳng nên $R' = R =2$. Bây giờ ta tìm toạ độ của tâm $I'$.
Giả sử $I'\left( {x';y'} \right) \Rightarrow \overrightarrow {OI'} = \left( {x';y'} \right)$. Ta cũng có $\overrightarrow {OI} = \left( {1;2} \right)$. Với góc quay là $60^o$, kết hợp với công thức tính tích vô hướng ta có $$\left( {\overrightarrow {OI} ,\overrightarrow {OI'} } \right) = {60^o} \Leftrightarrow \overrightarrow {OI} \cdot \overrightarrow {OI'} = OI \cdot OI'\cos {60^o} \Leftrightarrow x' + 2y' = \frac{5}{2} \Leftrightarrow x' = \frac{5}{2} - 2y'. \;\;\;\;\;\;\;\;\left( 1 \right)$$ Mặt khác ta cũng có $$OI' = OI = \sqrt 5 \Leftrightarrow \sqrt {{{x'}^2} + {{y'}^2}} = \sqrt 5 \Leftrightarrow {{x'}^2} + {{y'}^2} = 5.\;\;\;\;\;\;\;\;\left( 2 \right)$$ Kết hợp $(1)$ và $(2)$ ta có $${\left( {\frac{5}{2} - 2y'} \right)^2} + {{y'}^2} = 5 \Leftrightarrow \left[ \begin{gathered} y' = 1 + \frac{{\sqrt 3 }}{2}\;\;\;\; \hbox{(nhận)} \hfill \\ y' = 1 - \frac{{\sqrt 3 }}{2}\;\;\;\; \hbox{(loại)} \hfill \\ \end{gathered} \right..$$
Thay $y' = 1 + \frac{{\sqrt 3 }}{2}$ vào $(1)$ ta được $x' = \frac{1}{2} + \sqrt 3 $. Suy ra toạ độ tâm $I'\left( {\frac{1}{2} + \sqrt 3 ;1 + \frac{{\sqrt 3 }}{2}} \right)$. Suy ra $$\left( {C'} \right):{\left( {x - \frac{1}{2} - \sqrt 3 } \right)^2} + {\left( {y - 1 - \frac{{\sqrt 3 }}{2}} \right)^2} = 4.$$
Nếu đưa về hệ toạ độ cực, có thể việc tìm ảnh qua phép quay sẽ "tiện" hơn. Vấn đề này ta sẽ bàn kĩ hơn ở bài sau.
Bài tập
(nhiều bài tập hơn khi đăng ký học tại Trung tâm Cùng học toán)
Tác giả bài viết: Cùng Học Toán




Góp ý hoặc một bài toán của Quý học viên hoặc Quý Phụ Huynh