Tỷ mỷ làm toán. Độc lập suy nghĩ.
Tỷ mỷ làm toán. Độc lập suy nghĩ.
Hình chiếu vuông góc của điểm lên mặt phẳng
Hình chiếu vuông góc của điểm lên mặt phẳng. Tìm toạ độ hình chiếu vuông góc của điểm lên mặt phẳng.
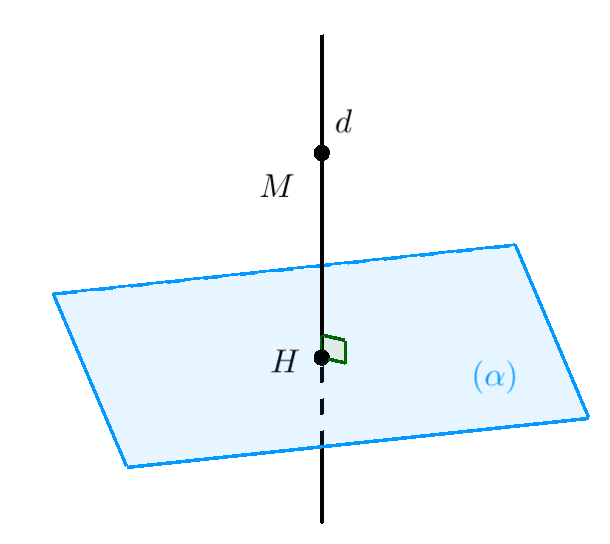
Hình chiếu vuông góc của điểm lên mặt phẳng. Để tìm hình chiếu vuông góc của điểm $M$ lên mặt phẳng $(\alpha)$ ta tiến hành các bước sau
Bước 1: Viết phương trình đường thẳng $d$ qua $M$ và vuông góc với $(\alpha)$.
Bước 2: Tìm toạ độ hình chiếu $H = d \cap \left( \alpha \right).$
Ví dụ. Tìm hình chiếu vuông góc của $M\left( {2;1;3} \right)$ lên mặt phẳng $\left( \alpha \right):x - y + z - 1 = 0.$
Giải. Bước 1: Viết phương trình đường thẳng $d$ qua $M$ và vuông góc với $(\alpha)$.
Ta có ${\vec u_d} = {\vec n_\alpha } = \left( {1; - 1;1} \right).$ Phương trình đường thẳng $d$ là $\left\{ \begin{array}{l}
x = 2 + t\\
y = 1 - t\\
z = 3 + t
\end{array} \right..$
Bước 2: Tìm toạ độ hình chiếu $H = d \cap \left( \alpha \right).$
Thay $x = 2 + t,y = 1 - t,z = 3 + t$ vào phương trình của $(\alpha)$ ta được $x = 1;y = 2;z = 2.$
Vậy hình chiếu vuông góc của điểm $M\left( {2;1;3} \right)$ lên mặt phẳng $\left( \alpha \right) $ là $H\left( {1;2;2} \right).$
Ta có ${\vec u_d} = {\vec n_\alpha } = \left( {1; - 1;1} \right).$ Phương trình đường thẳng $d$ là $\left\{ \begin{array}{l}
x = 2 + t\\
y = 1 - t\\
z = 3 + t
\end{array} \right..$
Bước 2: Tìm toạ độ hình chiếu $H = d \cap \left( \alpha \right).$
Thay $x = 2 + t,y = 1 - t,z = 3 + t$ vào phương trình của $(\alpha)$ ta được $x = 1;y = 2;z = 2.$
Vậy hình chiếu vuông góc của điểm $M\left( {2;1;3} \right)$ lên mặt phẳng $\left( \alpha \right) $ là $H\left( {1;2;2} \right).$
Bài tập
Tác giả bài viết: TT. Cùng Học Toán
Góp ý hoặc một bài toán của Quý học viên hoặc Quý Phụ Huynh