Tỷ mỷ làm toán. Độc lập suy nghĩ.

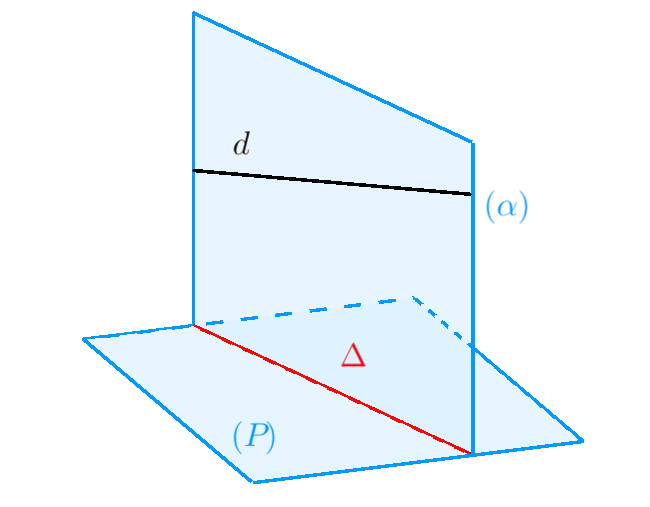
Step 1. Write the equation of the plane $(\alpha)$ that contains $d$ and is perpendicular to $(P)$. The pair of direction vectors for $(\alpha)$ is $\vec{n}_P$ and $\vec{u}_d$.

Step 2. Write the equation of the line $\Delta = (\alpha) \cap (P)$.
 

Example. Given (d):{x=1−ty=2+2tz=−1−t(d):\left\{ \begin{array}{l} x = 1 - t\\ y = 2 + 2t\\ z = -1 - t \end{array} \right.(d):⎩⎨⎧​x=1−ty=2+2tz=−1−t​ and (P):x−y+z−1=0.(P): x - y + z - 1 = 0.(P):x−y+z−1=0.

Write the parametric equations of the line $\Delta$, which is the orthogonal projection of $d$ onto $(P)$.
 
 

**Solution.**

**Step 1.** Let \((\alpha)\) be the plane containing \(d\) and perpendicular to \((P)\). The pair of direction vectors for \((\alpha)\) is \(\vec{u}_d = (-1; 2; -1)\), \(\vec{n}_P = (1; -1; 1)\). It follows that \(\vec{n}_\alpha = [\vec{u}_d, \vec{n}_P] = (1; 0; -1)\). Choose \(M(1; 2; -1) \in d \subset (\alpha)\).

The equation of the plane \((\alpha)\) is \((x - 1) + 0(y - 2) - 1(z + 1) = 0 \Leftrightarrow x - z - 2 = 0\).

**Step 2.** The orthogonal projection of \(d\) onto the plane \((P)\) is \(\Delta = (\alpha) \cap (P)\).

Thus, the general equation of \(\Delta\) is
\[
(\Delta): \left\{ \begin{array}{l}
x - y + z - 1 = 0 \\
x - z - 2 = 0
\end{array} \right..
\]

From here, we have the pair of normal vectors for \(\Delta\): \(\vec{n}_1 = (1; -1; 1)\), \(\vec{n}_2 = (1; 0; -1) \Rightarrow \vec{u}_\Delta = [\vec{n}_1, \vec{n}_2] = (1; 2; 1)\).

From the general equation of \(\Delta\), substitute \(x = 0 \Rightarrow y = -3\), \(z = -2 \Rightarrow A(0; -3; -2) \in \Delta\).

It follows that the parametric equations of \(\Delta\) are
\[
(\Delta): \left\{ \begin{array}{l}
x = t \\
y = -3 + 2t \\
z = -2 + t
\end{array} \right..
\]