Đường thẳng đi qua hai điểm cực trị hàm bậc ba
Đường thẳng đi qua hai điểm cực trị của hàm bậc ba. Phương trình đường thẳng đi qua hai điểm cực trị.
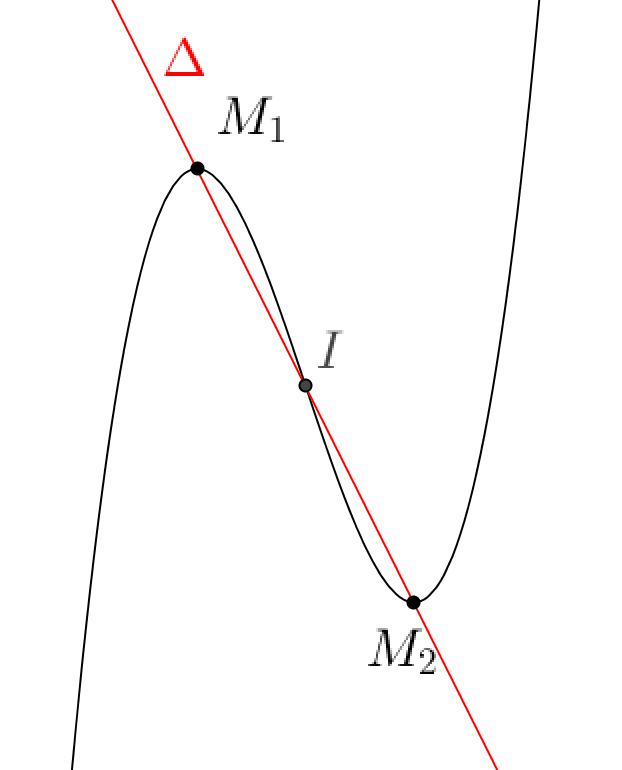
Cách 1. Tìm hai điểm cực trị $M_1$ và $M_2$ và viết phương trình $\Delta$.
Cách 2. Chia $y$ cho $y'$. Học sinh sẽ hiểu rõ hơn cách làm này qua ví dụ sau đây.
Ví dụ 1. Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số $y = {x^3} - 3x + 2$.
Giải. Ta có $y' = 3{x^2} - 3.$
Cách 1. Hoành độ hai điểm cực trị là nghiệm của phương trình $$y' = 0 \Leftrightarrow 3{x^2} - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}
{x_1} = 1 \Rightarrow {y_1} = 0\\
{x_2} = - 1 \Rightarrow {y_2} = 4
\end{array} \right.$$ Vậy hai điểm cực trị là ${M_1}\left( {1;0} \right)$ và ${M_2}\left( { - 1;4} \right).$ Phương trình đường thẳng $\Delta$ đi qua hai điểm cực trị là $$\begin{array}{c}
\frac{{x - {x_1}}}{{{x_2} - {x_1}}} = \frac{{y - {y_1}}}{{{y_2} - {y_1}}} \Leftrightarrow \frac{{x - 1}}{{ - 1 - 1}} = \frac{{y - 0}}{{4 - 0}}\\
\Leftrightarrow 2x + y - 2 = 0.
\end{array}$$ Vậy phương trình đường thẳng đi qua hai điểm cực trị là $\Delta :\;\;2x + y - 2 = 0.$
Cách 2. Chia $y$ cho $y'$ ta được $$y = \left( {\frac{1}{3}x} \right) \cdot y' + \left( { - 2x + 2} \right).$$ Vì ${M_1}\left( {{x_1};{y_1}} \right) \in \left( C \right)$ nên $$\begin{array}{l}
{y_1} = \left( {\frac{1}{3}{x_1}} \right) \cdot \underbrace {y'\left( {{x_1}} \right)}_{ = 0} + \left( { - 2{x_1} + 2} \right)\,.\\
\,\,\,\,\,\,\, \Leftrightarrow {y_1} = - 2{x_1} + 2.\\
\,\,\,\,\,\,\, \Rightarrow {M_1} \in \Delta :y = - 2x + 2.
\end{array}$$ Tương tự ta cũng có ${M_2} \in \Delta :y = - 2x + 2$.
Vậy đường thẳng đi qua hai điểm cực trị là $\Delta :\;\;2x + y - 2 = 0.$
Cách 1. Hoành độ hai điểm cực trị là nghiệm của phương trình $$y' = 0 \Leftrightarrow 3{x^2} - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}
{x_1} = 1 \Rightarrow {y_1} = 0\\
{x_2} = - 1 \Rightarrow {y_2} = 4
\end{array} \right.$$ Vậy hai điểm cực trị là ${M_1}\left( {1;0} \right)$ và ${M_2}\left( { - 1;4} \right).$ Phương trình đường thẳng $\Delta$ đi qua hai điểm cực trị là $$\begin{array}{c}
\frac{{x - {x_1}}}{{{x_2} - {x_1}}} = \frac{{y - {y_1}}}{{{y_2} - {y_1}}} \Leftrightarrow \frac{{x - 1}}{{ - 1 - 1}} = \frac{{y - 0}}{{4 - 0}}\\
\Leftrightarrow 2x + y - 2 = 0.
\end{array}$$ Vậy phương trình đường thẳng đi qua hai điểm cực trị là $\Delta :\;\;2x + y - 2 = 0.$
Cách 2. Chia $y$ cho $y'$ ta được $$y = \left( {\frac{1}{3}x} \right) \cdot y' + \left( { - 2x + 2} \right).$$ Vì ${M_1}\left( {{x_1};{y_1}} \right) \in \left( C \right)$ nên $$\begin{array}{l}
{y_1} = \left( {\frac{1}{3}{x_1}} \right) \cdot \underbrace {y'\left( {{x_1}} \right)}_{ = 0} + \left( { - 2{x_1} + 2} \right)\,.\\
\,\,\,\,\,\,\, \Leftrightarrow {y_1} = - 2{x_1} + 2.\\
\,\,\,\,\,\,\, \Rightarrow {M_1} \in \Delta :y = - 2x + 2.
\end{array}$$ Tương tự ta cũng có ${M_2} \in \Delta :y = - 2x + 2$.
Vậy đường thẳng đi qua hai điểm cực trị là $\Delta :\;\;2x + y - 2 = 0.$
Bình luận. Theo cách 2, ta thấy phương trình của đường thẳng đi qua hai điểm cực trị được lập bởi phần dư trong phép chia $y$ cho $y'$.
Ví dụ 2. Định $m$ để hàm số $y = 2{x^3} + 3m{x^2} - 12{m^2}x + m + 2$ có hai cực trị và viết phương trình đường thẳng đi qua hai điểm cực trị.
Ví dụ 2. Định $m$ để hàm số $y = 2{x^3} + 3m{x^2} - 12{m^2}x + m + 2$ có hai cực trị và viết phương trình đường thẳng đi qua hai điểm cực trị.
Giải. Ta có $y' = 6{x^2} + 6mx - 12{m^2}$. Hàm số có hai cực trị khi $${{\Delta '}_{y'}} > 0 \Leftrightarrow {\left( {3m} \right)^2} - 6\left( { - 12{m^2}} \right) > 0 \Leftrightarrow 81{m^2} > 0 \Leftrightarrow m \ne 0.$$ Bây giờ ta viết phương trình đường thảng $\Delta$ đi qua hai điểm cực trị theo $2$ cách.
Cách 1. Ta có $$y' = 0 \Leftrightarrow 6\left( {x - m} \right)\left( {x + 2m} \right) = 0 \Leftrightarrow \left[ \begin{gathered}
x = m\;\;\;\;\;\; \Rightarrow y = - 7{m^3} + m + 2 \hfill \\
x = - 2m\;\; \Rightarrow y = 20{m^3} + m + 2\; \hfill \\
\end{gathered} \right.$$
Vậy hai điểm cực trị là ${M_1}\left( {m; - 7{m^3} + m + 2} \right),{M_2}\left( { - 2m;20{m^3} + m + 2} \right)$. Từ đây ta có phương trình đường thẳng $\Delta$ đi qua hai điểm cực trị là $$\Delta :y = {m^2}x + 2{m^3} + m + 2,\;\;m \ne 0.$$
Cách 2. Chi $y$ cho $y'$ ta được $$y = \left( {{x \over 3} + {m \over 6}} \right)y' + {m^2}x + 2{m^3} + m + 2.$$ Vậy phương trình đường thẳng $\Delta$ đi qua hai điểm cực trị là $$\Delta :y = {m^2}x + 2{m^3} + m + 2,\;\;m \ne 0.$$
Cách 1. Ta có $$y' = 0 \Leftrightarrow 6\left( {x - m} \right)\left( {x + 2m} \right) = 0 \Leftrightarrow \left[ \begin{gathered}
x = m\;\;\;\;\;\; \Rightarrow y = - 7{m^3} + m + 2 \hfill \\
x = - 2m\;\; \Rightarrow y = 20{m^3} + m + 2\; \hfill \\
\end{gathered} \right.$$
Vậy hai điểm cực trị là ${M_1}\left( {m; - 7{m^3} + m + 2} \right),{M_2}\left( { - 2m;20{m^3} + m + 2} \right)$. Từ đây ta có phương trình đường thẳng $\Delta$ đi qua hai điểm cực trị là $$\Delta :y = {m^2}x + 2{m^3} + m + 2,\;\;m \ne 0.$$
Cách 2. Chi $y$ cho $y'$ ta được $$y = \left( {{x \over 3} + {m \over 6}} \right)y' + {m^2}x + 2{m^3} + m + 2.$$ Vậy phương trình đường thẳng $\Delta$ đi qua hai điểm cực trị là $$\Delta :y = {m^2}x + 2{m^3} + m + 2,\;\;m \ne 0.$$
Bình luận. Theo cách 1, để viết được phương trình của $\Delta$, ta phải biết toạ độ điểm cực trị; còn ở cách 2 ta không cần biết toạ độ của hai điểm cực trị. Đó là lợi thế của cách 2, nhất là đối với những bài có chứa tham số, như ví dụ trên chẳng hạn. Hơn nữa, cách 1 ở ví dụ trên khá dài dòng, chưa kể đến chuyện nếu như toạ độ của điểm cực trị có chứa căn thức! Như vậy, khi viết phương trình đường thẳng đi qua hai điểm cực trị, ta nên dùng cách 2 nếu hàm số có chứa tham số, nhưng đừng quên tìm điều kiện để hàm số có hai cực trị !
(nhiều bài tập hơn khi đăng ký học tại Trung tâm Cùng học toán)
Bài tập
(nhiều bài tập hơn khi đăng ký học tại Trung tâm Cùng học toán)
Tác giả bài viết: Cùng Học Toán




Góp ý hoặc một bài toán của Quý học viên hoặc Quý Phụ Huynh