Phương trình tiếp tuyến tại một điểm

Thứ sáu - 12/02/2016 22:00
Viết phương trình tiếp tuyến của đồ thị hàm số tại một điểm.
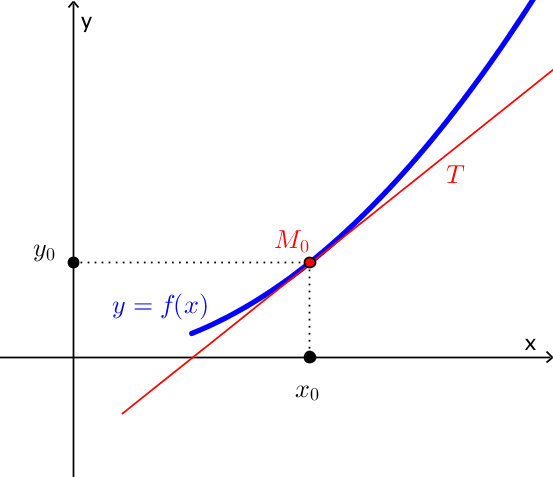
tieptuyen



 
 Phương trình tiếp tuyến $\Delta$ của hàm số $y=f\left( x \right)$  tại điểm $M_0(x_0;y_0)$ là
$$y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + {y_0}.\;\;$$











 
 
Ví dụ 1


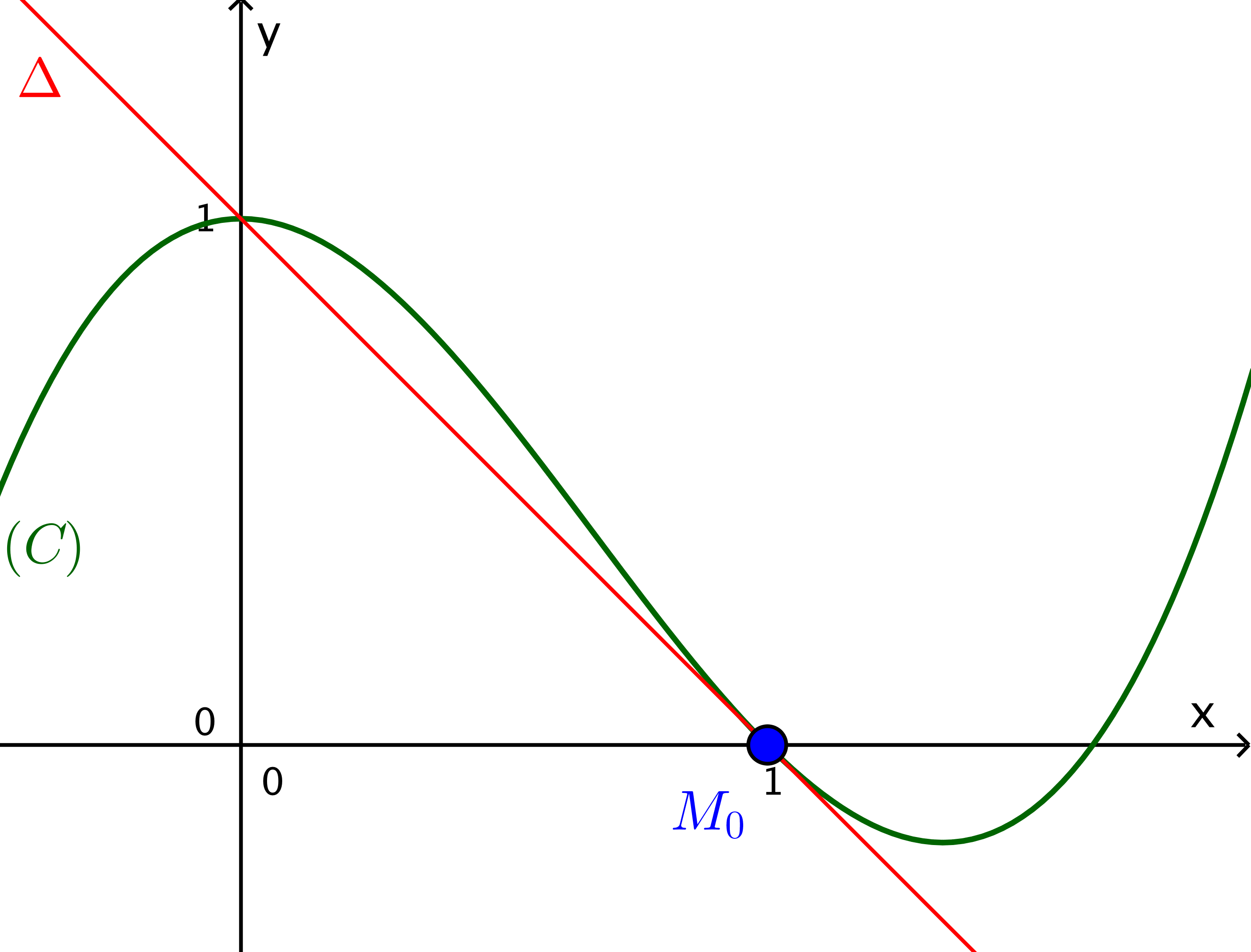
Ví dụ 1. Viết phương trình tiếp tuyến của đồ thị hàm số   $f\left( x \right) = {x^3} - 2{x^2} + 1$ tại ${M_0}\left( {1;0} \right).$

Giải. Ta có $f'\left( x \right) = 3{x^2} - 4x \Rightarrow f'\left( {{x_0}} \right) = f'\left( 1 \right) =  - 1.$ Phương trình tiếp tuyến tại ${M_0}\left( {1;0} \right)$ là $$ (\Delta): y =  - \left( {x - 1} \right) + 0 \Leftrightarrow y =  - x + 1.$$




 

 
 

 
Ví dụ 2

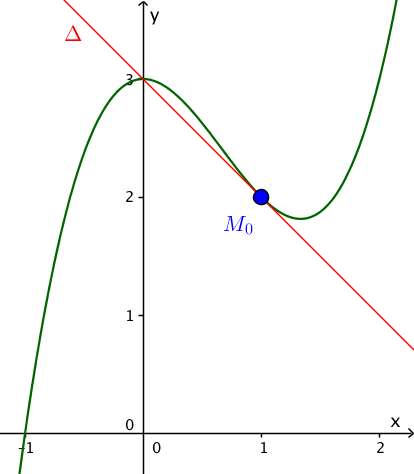
Ví dụ 2. Viết phương trình tiếp tuyến của đồ thị hàm số $f\left( x \right) = {x^3} - 2x + 3$ tại điểm có hoành độ ${x_0} = 1.$

Giải. Với ${x_0} = 1 \Rightarrow {y_0} = f\left( {{x_0}} \right) = 2 \Rightarrow $ tiếp điểm ${M_0}\left( {1;2} \right).$
Ta có $f'\left( x \right) = 3{x^2} - 2 \Rightarrow f'\left( {{x_0}} \right) = f'\left( 1 \right) = 1.$
Phương trình tiếp tuyến tại ${M_0}\left( {1;2} \right)$ là $$(\Delta): y = \left( {x - 1} \right) + 2 \Leftrightarrow y = x + 1.$$







 
 

 
Ví dụ 3
Ví dụ 3. Viết phương trình tiếp tuyến của đồ thị hàm số $f\left( x \right) = {x^3} - 3x + 3$ tại điểm có tung độ ${y} = 1.$
 
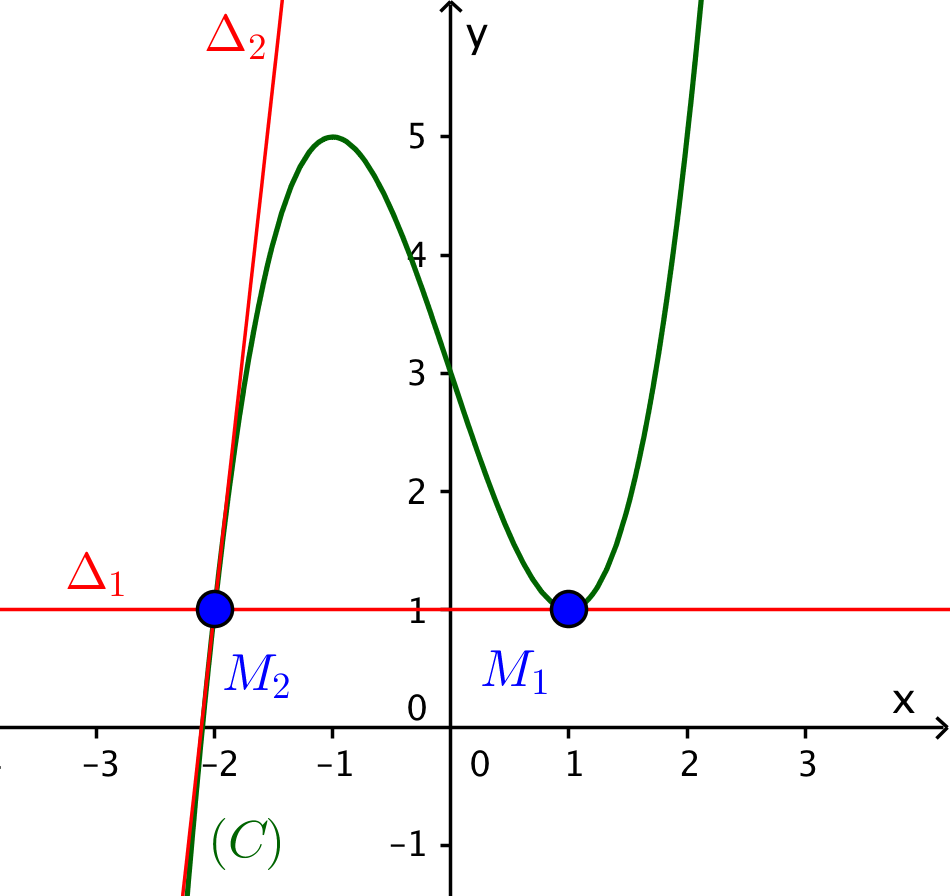
Giải. Với ${y} = 1 \Leftrightarrow {x^3} - 3x + 3 = 1 \Leftrightarrow \left[ \begin{array}{l}
x_1 = 1\\
x_2 =  - 2
\end{array} \right. \Rightarrow $ các tiếp điểm là ${M_1}\left( {1;1} \right),{M_2}\left( { - 2;1} \right).$
Ta có $f'\left( x \right) = 3{x^2} - 3.$
 
$\bullet$ Tại ${M_1}\left( {1;1} \right)$, ta có $f'\left( {{x_1}} \right) = f'\left( 1 \right) = 0$. Phương trình tiếp tuyến tại ${M_1}\left( {1;1} \right)$ là $$\left( {{\Delta_1}} \right):\;\;\;\;y = f'\left( {{x_1}} \right)\left( {x - {x_1}} \right) + {y_1} \Leftrightarrow y = 0\left( {x - 1} \right) + 1 \Leftrightarrow y = 1.$$

$\bullet$ Tại ${M_2}\left( { - 2;1} \right)$, ta có $f'\left( {{x_2}} \right) = f'\left( { - 2} \right) = 9$. Phương trình tiếp tuyến tại ${M_2}\left( { - 2;1} \right)$ là $$\left( {{\Delta_2}} \right):\;\;\;\;y = f'\left( {{x_2}} \right)\left( {x - {x_2}} \right) + {y_2} \Leftrightarrow y = 9\left( {x + 2} \right) + 1 \Leftrightarrow y = 9x + 19.$$
 


 
 


 
 
Ví dụ 4

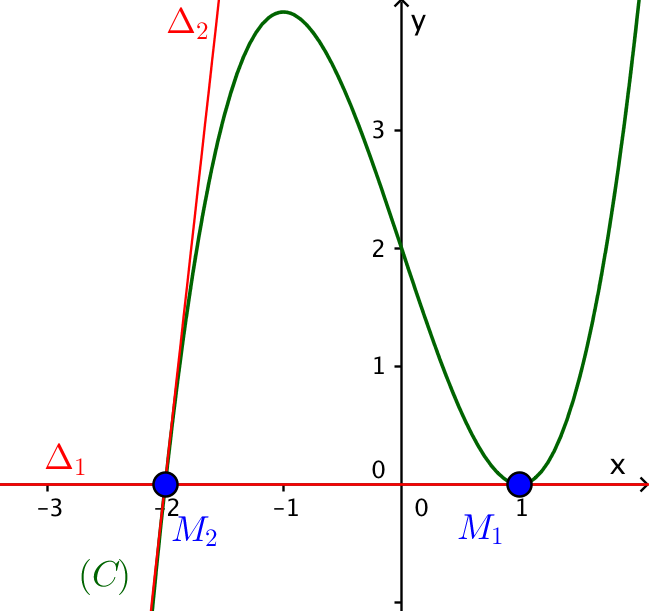
Ví dụ 4. Viết phương trình tiếp tuyến của đồ thị hàm số $f\left( x \right) = {x^3} - 3x + 2$ tại giao điểm của đồ thị hàm số với trục hoành.
 
Giải. Hoành độ giao điểm của đồ thị hàm số và trục hoành là nghiệm của phương trình $$f\left( x \right) = 0 \Leftrightarrow {x^3} - 3x + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}
{x_1} =  1\\
{x_2} = -2
\end{array} \right..$$ Suy ra các tiếp điểm là ${M_1}\left( {1;0} \right),{M_2}\left( { - 2;0} \right).$
Ta có $f'\left( x \right) = 3{x^2} - 3.$
 
$\bullet$ Tại ${M_1}\left( {1;0} \right)$, ta có $f'\left( {{x_1}} \right) = f'\left( 1 \right) = 0$. Phương trình tiếp tuyến tại ${M_1}\left( {1;0} \right)$ là $$\left( {{\Delta_1}} \right):\;\;\;\;y = f'\left( {{x_1}} \right)\left( {x - {x_1}} \right) + {y_1} \Leftrightarrow y = 0\left( {x - 1} \right) + 0 \Leftrightarrow y = 0.$$

$\bullet$ Tại ${M_2}\left( { - 2;0} \right)$, ta có $f'\left( {{x_2}} \right) = f'\left( { - 2} \right) = 9$. Phương trình tiếp tuyến tại ${M_2}\left( { - 2;1} \right)$ là $$\left( {{\Delta_2}} \right):\;\;\;\;y = f'\left( {{x_2}} \right)\left( {x - {x_2}} \right) + {y_2} \Leftrightarrow y = 9\left( {x + 2} \right) + 0 \Leftrightarrow y = 9x + 18.$$
 
 



 
Bài tập 

(nhiều bài tập hơn khi đăng ký học tại Trung tâm Cùng học toán)

 

Tác giả bài viết: TT. Cùng Học Toán

Tổng số điểm của bài viết là: 0 trong 0 đánh giá

Click để đánh giá bài viết

  Góp ý hoặc một bài toán của Quý học viên hoặc Quý Phụ Huynh

Mã bảo mật   

Những tin mới hơn

Bài viết cùng chuyên mục

Chương trình
Thư viện trực tuyến
Kiến thức mới
Thư viện trực tuyến