Điều kiện tiếp xúc của hai đồ thị
Đồ thị tiếp xúc của hai đồ thị hàm số.
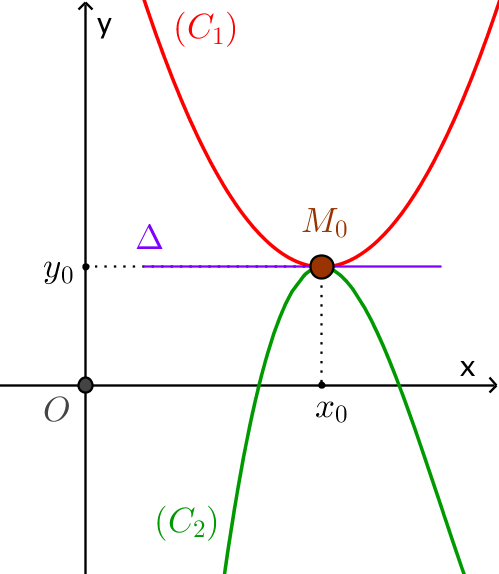
Điều kiện tiếp xúc của hai đồ thị hàm số. Điều kiện để hai đồ thị $\left( {{C_1}} \right):y = f\left( x \right)$ và $\left( {{C_2}} \right):y = g\left( x \right)$ tiếp xúc nhau là chúng có chung ít nhất $1$ tiếp tuyến $\Delta$. Nghĩa là hệ sau có ít nhất một nghiệm $$\left\{ \begin{array}{l} f\left( x \right) = g\left( x \right){\rm{ }}\left( 1 \right)\\ f'\left( x \right) = g'\left( x \right){\rm{ }}\left( 2 \right) \end{array} \right.$$
Nghiệm $x_0$ của hệ, nếu có, cũng là hoành độ của tiếp điểm $M_0$.
- $(1)$ là phương trình hoành độ giao điểm của $\left( {{C_1}} \right)$ và $\left( {{C_2}} \right)$. Phương trình này có nghiệm tức là hai đồ thị $\left( {{C_1}} \right)$ và $\left( {{C_2}} \right)$ có điểm chung. Tuy nhiên điểm chung này chưa hẳn là tiếp điểm.
- $(2)$ có nghiệm tức là hai đường cong $\left( {{C_1}} \right)$ và $\left( {{C_2}} \right)$ có chung tiếp tuyến $\Delta$. Khi đó hệ số góc của tiếp tuyến này chính là $f'\left( {{x_0}} \right) = g'\left( {{x_0}} \right)$. Đây chính là ràng buộc cho những điểm chung, nếu có, của $\left( {{C_1}} \right)$ và $\left( {{C_2}} \right)$ trở thành tiếp điểm.
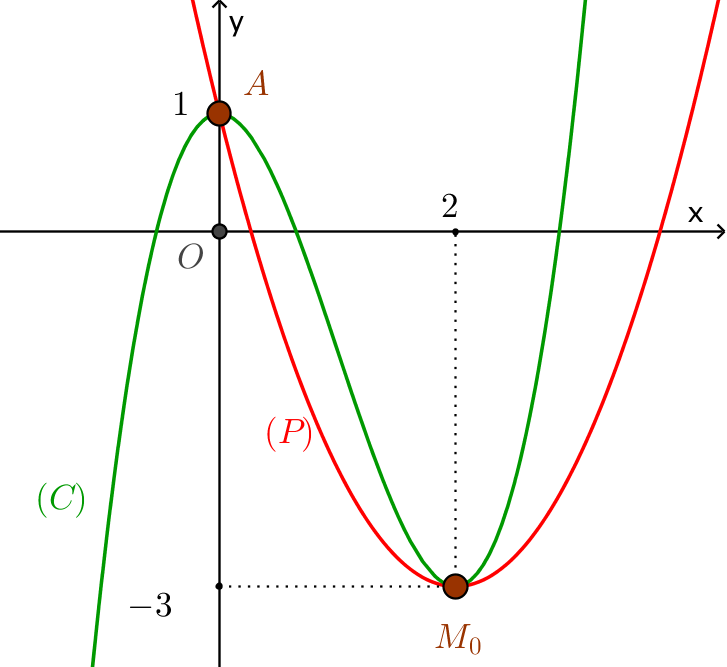
Ví dụ 1. Cho parabol $\left( P \right):f\left( x \right) = {x^2} - 4x + 1$ và đường cong $g\left( x \right) = {x^3} - 3{x^2} + 1$. Hãy tìm các giao điểm của $\left( P \right)$ và $\left( C \right)$ đồng thời cho biết trong số các điểm chung này đâu là tiếp điểm.
Giải. Ta có $f'\left( x \right) = 2x - 4$ và $g'\left( x \right) = 3{x^2} - 6x$. $\left( P \right)$ và $\left( C \right)$ tiếp xúc nhau khi hệ sau đây có nghiệm $$\left\{ \begin{array}{l} f\left( x \right) = g\left( x \right)\\ f'\left( x \right) = g'\left( x \right) \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} {x^2} - 4x + 1 = {x^3} - 3{x^2} + 1\\ 2x - 4 = 3{x^2} - 6x \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} {x^3} - 4{x^2} + 4x = 0{\rm{ }}\left( 1 \right)\\ 3{x^2} - 8x + 4 = 0{\rm{ }}\left( 2 \right) \end{array} \right..$$
Ta có $\left( 1 \right) \Leftrightarrow x{\left( {x - 2} \right)^2} \Leftrightarrow \left[ \begin{array}{l} x = 0 \Rightarrow y = 1\\ x = 2 \Rightarrow y =- 3. \end{array} \right.$
Vì $(1)$ là phương trình hoành độ giao điểm của $\left( P \right)$ và $\left( C \right)$ nên từ kết quả này ta suy ra $\left( P \right)$ cắt $\left( C \right)$ tại hai điểm là $A\left( {0;1} \right)$ và ${M_0}\left( {2; - 3} \right)$.
Trong $2$ nghiệm của $(1)$ chỉ có nghiệm $x=2$ là thoả phương trình $(2)$. Như vậy điểm ${M_0}\left( {2; - 3} \right)$ chính là tiếp điểm của $\left( P \right)$ và $\left( C \right)$.
Ví dụ 2. Xác định $k$ để đồ thị hàm số $ f\left( x \right) = {x^3} - 3x + 1$ nhận đường thẳng $\left( d \right):y = k\left( {x - 1} \right) - 1$ làm tiếp tuyến. Tìm tọa độ tiếp điểm.
Giải. Đường thẳng $d$ tiếp xúc với đồ thị hàm số khi hệ sau có nghiệm $$\left\{ \begin{array}{l}
{x^3} - 3x + 1 = k\left( {x - 1} \right) - 1\,\,\,\,\,\,\,\,\left( 1 \right)\\
3{x^2} - 3 = k\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)
\end{array} \right.$$ Thay $\left( 2 \right)$ vào $\left( 1 \right)$ ta được $${x^3} - 3x + 1 = \left( {3{x^2} - 3} \right)\left( {x - 1} \right) - 1 \Leftrightarrow 2{x^3} - 3{x^2} + 1 = 0 \Leftrightarrow \left[ \begin{array}{l}
x = - \frac{1}{2}\\
x = 1.
\end{array} \right.$$ Với $x = - \frac{1}{2} \Rightarrow y = - \frac{5}{8} \Rightarrow {M_1}\left( { - \frac{1}{2}; - \frac{5}{8}} \right),{k_1} = - \frac{9}{4}.$ Suy ra tiếp tuyến $$\left( {{d_1}} \right):y = - \frac{9}{4}\left( {x - \frac{1}{2}} \right) - \frac{5}{8} \Leftrightarrow y = - \frac{9}{4}x + \frac{5}{4}.$$
Với $x = 1 \Rightarrow y = - 1 \Rightarrow {M_2}\left( {1; - 1} \right),{k_2} = 0.$ Suy ra tiếp tuyến $$\left( {{d_2}} \right):y = 0\left( {x - 1} \right) - 1 \Leftrightarrow y = - 1.$$
{x^3} - 3x + 1 = k\left( {x - 1} \right) - 1\,\,\,\,\,\,\,\,\left( 1 \right)\\
3{x^2} - 3 = k\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)
\end{array} \right.$$ Thay $\left( 2 \right)$ vào $\left( 1 \right)$ ta được $${x^3} - 3x + 1 = \left( {3{x^2} - 3} \right)\left( {x - 1} \right) - 1 \Leftrightarrow 2{x^3} - 3{x^2} + 1 = 0 \Leftrightarrow \left[ \begin{array}{l}
x = - \frac{1}{2}\\
x = 1.
\end{array} \right.$$ Với $x = - \frac{1}{2} \Rightarrow y = - \frac{5}{8} \Rightarrow {M_1}\left( { - \frac{1}{2}; - \frac{5}{8}} \right),{k_1} = - \frac{9}{4}.$ Suy ra tiếp tuyến $$\left( {{d_1}} \right):y = - \frac{9}{4}\left( {x - \frac{1}{2}} \right) - \frac{5}{8} \Leftrightarrow y = - \frac{9}{4}x + \frac{5}{4}.$$
Với $x = 1 \Rightarrow y = - 1 \Rightarrow {M_2}\left( {1; - 1} \right),{k_2} = 0.$ Suy ra tiếp tuyến $$\left( {{d_2}} \right):y = 0\left( {x - 1} \right) - 1 \Leftrightarrow y = - 1.$$
Ví dụ 3. Xác định $m$ để đồ thị hàm số $(C): y = {x^3} + m{x^2} - 9x - 9m$ tiếp xúc với trục hoành.
Giải. Phương trình của trục hoành: $y = 0$. Đồ thị $( C )$ tiếp xúc với trục hoành khi hệ sau có nghiệm $$\left\{ \begin{array}{l} {x^3} + m{x^2} - 9x - 9m = 0\left( 1 \right)\\ 3{x^2} + 2mx - 9 = 0\left( 2 \right) \end{array} \right.$$ $\left( 1 \right) \Leftrightarrow {x^3} + m{x^2} - 9x - 9m = 0 \Leftrightarrow \left( {x - 3} \right)\left( {x + 3} \right)\left( {m + x} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}
x = 3\\
x = - 3\\
x = - m
\end{array} \right.$
Thay $x=3$ vào $\left( 2 \right) $ ta được $m=-3$.
Thay $x=-3$ vào $\left( 2 \right) $ ta được $m=3$.
Thay $x=-m$ vào $\left( 2 \right) $ ta được ${m^2} = 9 \Leftrightarrow m = \pm 3$.
Vậy với $m=3$ hoặc $m=-3$ thì đồ thị hàm số tiếp xúc với trục hoành.
x = 3\\
x = - 3\\
x = - m
\end{array} \right.$
Thay $x=3$ vào $\left( 2 \right) $ ta được $m=-3$.
Thay $x=-3$ vào $\left( 2 \right) $ ta được $m=3$.
Thay $x=-m$ vào $\left( 2 \right) $ ta được ${m^2} = 9 \Leftrightarrow m = \pm 3$.
Vậy với $m=3$ hoặc $m=-3$ thì đồ thị hàm số tiếp xúc với trục hoành.
Tác giả bài viết: Cùng Học Toán
Góp ý hoặc một bài toán của Quý học viên hoặc Quý Phụ Huynh




Cho hai hàm số y=(m+1)x^2+3m^2x+m và y=(m+1)x^2+12x+2. Tìm tất cả các giá trị của tham số m để đồ thị hai hàm số không cắt nhau
Tìm m để đồ thị hàm số y bằng x^3 trừ 3mx +m+1 tiếp xúc với trục hoành
giúp em với ạ đồ thị nào sau đây tiếp xúc với đường thẳng y=x-6 và có tâm đối xứng là I(1;-1) .
a. y = -x-3/x-1
b. y= x-3/x-1
c. x+3/x-1
d y=-x-3/x=1
viết lời giải giùm em ạ
giúp e vs ak......!
tìm m để đồ thị hàm số y = -2x^2 và y= -(2m + 1)x +m tiếp xúc với nhau khi đó tìm tọa độ tiếp điểm....
@Hien Chào Hien, bạn kiểm tra đề lại xem có gõ sai không?!