Tỷ mỷ làm toán. Độc lập suy nghĩ.
Tỷ mỷ làm toán. Độc lập suy nghĩ.
Đường tròn lượng giác
Đường tròn lượng giác. Chiều âm và chiều dương của đường tròn lượng giác. Định nghĩa các hàm lượng giác trên đường tròn lượng giác.
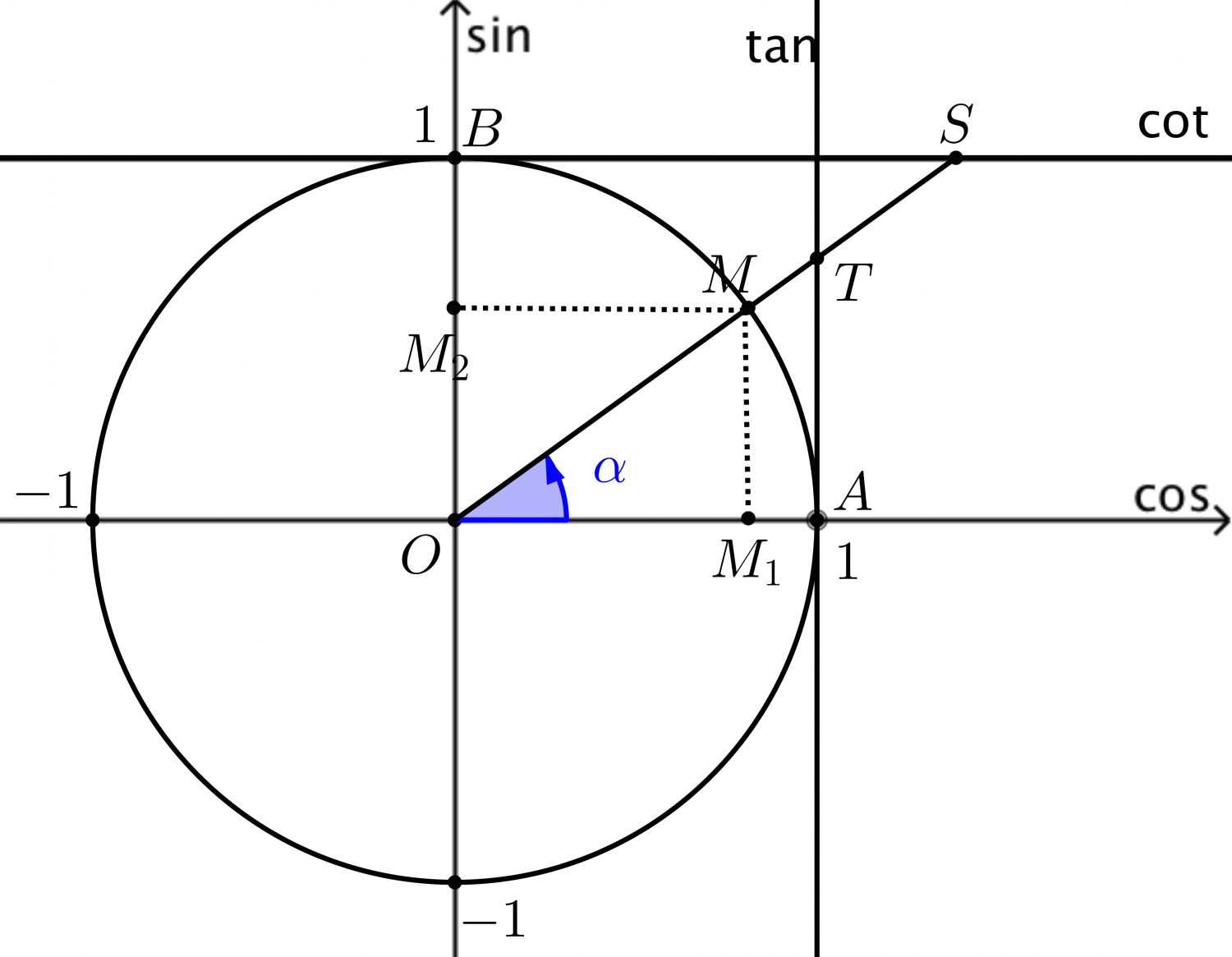
Trục hoành là trục cos, trục tung là trục sin.
Trục tan có gốc là điểm $A$ và vuông góc với trục cos, trục cotan có gốc là điểm $B$ vuông góc với trục sin.
Chiều dương là chiều ngược chiều kim đồng hồ, chiều âm cùng chiều kim đồng hồ.
Cho góc lượng giác $\alpha$ như trong Hình 1, ta có $$\begin{gathered}
\cos \alpha = \overline {O{M_1}} ,\;\;\;\;\sin \alpha = \overline {O{M_2}} , \hfill \\
\tan \alpha = \overline {AT} ,\;\;\;\;\;\;\cot \alpha = \overline {BS} , \hfill \\
\end{gathered} $$
\cos \alpha = \overline {O{M_1}} ,\;\;\;\;\sin \alpha = \overline {O{M_2}} , \hfill \\
\tan \alpha = \overline {AT} ,\;\;\;\;\;\;\cot \alpha = \overline {BS} , \hfill \\
\end{gathered} $$
trong đó ký hiệu $\overline {OM} $ dùng để chỉ độ dài đại số của $OM$.
Từ đây ta có $${\cos ^2}\alpha + {\sin ^2}\alpha = OM_1^2 + OM_2^2 = OM_1^2 + MM_1^2 = {R^2} = 1.$$
Bài tập
(nhiều bài tập hơn khi đăng ký học tại Trung tâm Cùng học toán)
Tác giả bài viết: Cùng Học Toán
Góp ý hoặc một bài toán của Quý học viên hoặc Quý Phụ Huynh
giải cứu
Hay