Tỷ mỷ làm toán. Độc lập suy nghĩ.
Tỷ mỷ làm toán. Độc lập suy nghĩ.
Hệ toạ độ Decart vuông góc
Hệ toạ độ Decart vuông góc trong không gian. Toạ độ của một vector. Toạ độ của một điểm.
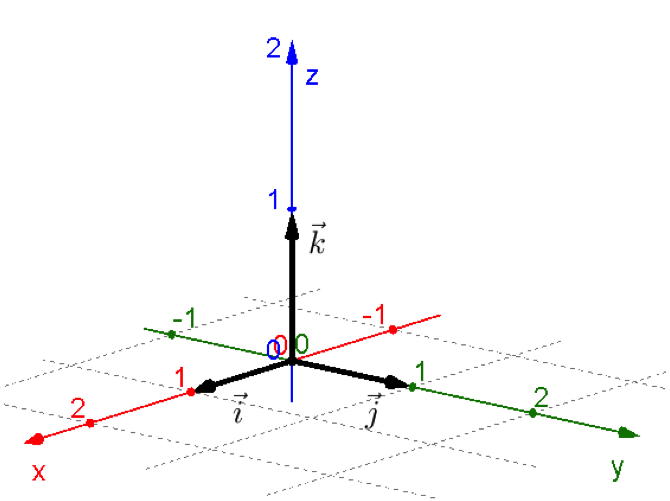
Hệ toạ độ Decart vuông góc. Trong không gian cho ba trục $Ox, Oy, Oz$ đôi một vuông góc với nhau tại gốc chung $O$. Gọi $\vec i,\vec j,\vec k$ là các vector đơn vị trên các trục $Ox, Oy, Oz$.
Các vector $\vec i,\vec j,\vec k$ có độ dài là $1$ và đôi một vuông góc với nhau.
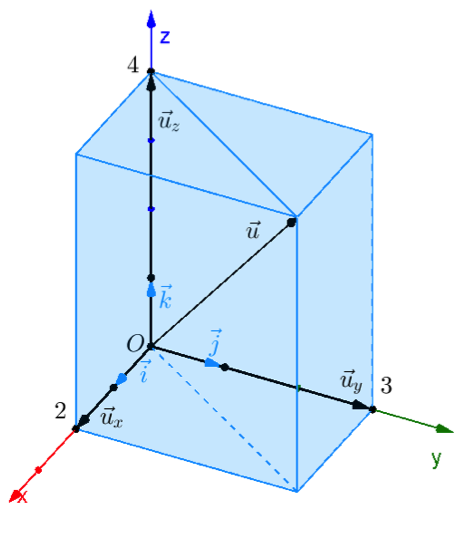
Toạ độ của vector trong không gian. Trong không gian tọa độ $Oxyz$ với các vector đơn vị $\vec i,\vec j,\vec k$ trên các trục toạ độ $Ox,Oy,Oz$ cho vector $\vec u.$ Khi đó tồn tại một bộ ba số thực $\left( {x;y;z} \right)$ sao cho $\vec u = x \vec i + y \vec j + z \vec k.$ Bộ ba số thực $\left( {x;y;z} \right)$ được gọi là toạ độ của vector $\vec u.$ và được ký hiệu là $\vec u = \left( {x;y;z} \right).$
Ví dụ 1. Trong Hình 2, gọi ${\vec u_x},{\vec u_y},{\vec u_z}$ lần lượt là hình chiếu vuông góc của vector $\vec u$ lên $Ox,Oy,Oz$. Rõ ràng ta có $${{\vec u}_x} = 2 \cdot \vec i;\;\;{{\vec u}_y} = 3 \cdot \vec j;\;\;{{\vec u}_z} = 4 \cdot \vec k.$$ Từ đây ta có $$\eqalign{
& \vec u = {{\vec u}_x} + {{\vec u}_y} + {{\vec u}_z} \cr
& \;\;\; = 2\vec i + 3\vec j + 4\vec k. \cr} $$ Như vậy toạ độ của vector $\vec u$ là $\left( {2;3;4} \right).$ Ta viết $\vec u = \left( {2;3;4} \right).$
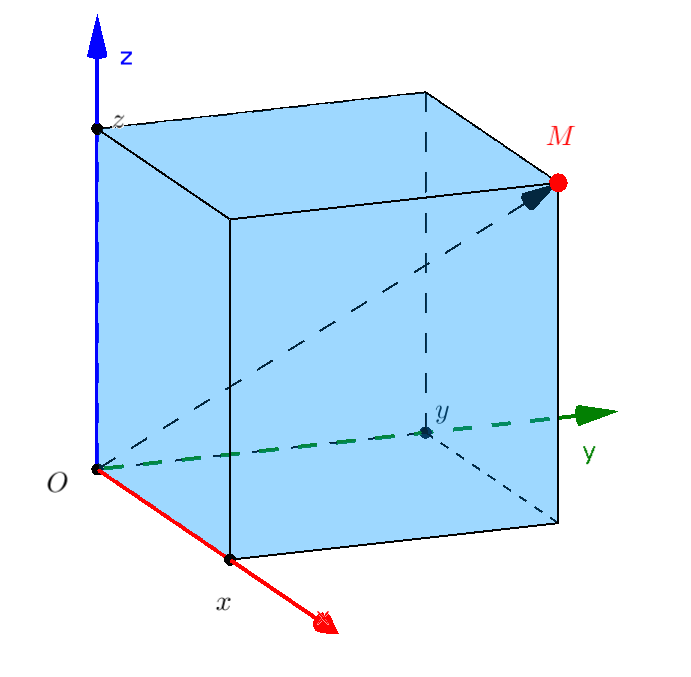
Toạ độ của một điểm trong không gian. Giả sử $M$ là một điểm trong không gian $Oxyz$. Nếu $\overrightarrow {OM} = \left( {x;y;z} \right)$ thì ta cũng nói bộ số $\left( {x;y;z} \right)$ là toạ độ của điểm $M$, kí hiệu $M\left( {x;y;z} \right)$ hay $M = \left( {x;y;z} \right).$
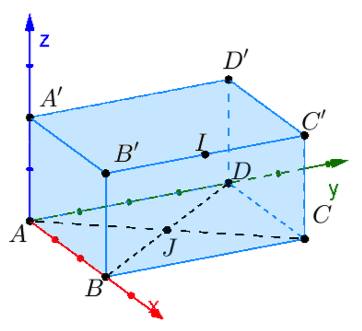
Ví dụ 2. Ở Hình 4, ta dễ thấy $$\eqalign{
& A\left( {0;0;0} \right),B\left( {3;0;0} \right),C\left( {3;4;0} \right), \cr
& D\left( {0;4;0} \right),D'\left( {0;4;2} \right),I\left( {3;2;2} \right). \cr} $$
Các bạn học sinh thử cho biết toạ độ của các điểm còn lại thử xem !
Form biểu diễn toạ độ của điểm trong không gian
Bài tập
(nhiều bài tập hơn khi đăng ký học tại Trung tâm Cùng học toán)
Tác giả bài viết: Cùng Học Toán
Góp ý hoặc một bài toán của Quý học viên hoặc Quý Phụ Huynh