Tỷ mỷ làm toán. Độc lập suy nghĩ.
Tỷ mỷ làm toán. Độc lập suy nghĩ.
Hàm số logarit
Định nghĩa hàm số logarit. Khảo sát và vẽ đồ thị hàm số logarit.
Định nghĩa. Hàm logarit có dạng $y = {\log _a}x$, trong đó $0<a \ne 1$, xác định với mợi $x>0$.
Ví dụ 1. $f\left( x \right) = {\log _2}x,\;\;\;g\left( x \right) = {\log _{\frac{1}{3}}}x.$
Khảo sát sự biến thiên của hàm số mũ. Ta xét hai trường hợp.
Ví dụ 2. Khảo sát và vẽ đồ thị hàm số $f\left( x \right) = {\log _2}x$.
Bài tập
(nhiều bài tập hơn khi đăng ký học tại Trung tâm Cùng học toán)
Ví dụ 1. $f\left( x \right) = {\log _2}x,\;\;\;g\left( x \right) = {\log _{\frac{1}{3}}}x.$
Khảo sát sự biến thiên của hàm số mũ. Ta xét hai trường hợp.
Trường hợp 1. $a>1$
$ \bullet $ Tập xác định $D = \left( {0; + \infty } \right).$
$ \bullet $ Sự biến thiên: Hàm số đồng biến trên khoảng $D = \left( {0; + \infty } \right).$
$ \bullet $ Giới hạn $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } {\log _a}x = + \infty .$
$\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} {\log _2}x = - \infty \Rightarrow $ $Oy$ là tiệm cận đứng.
$ \bullet $ Sự biến thiên: Hàm số đồng biến trên khoảng $D = \left( {0; + \infty } \right).$
$ \bullet $ Giới hạn $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } {\log _a}x = + \infty .$
$\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} {\log _2}x = - \infty \Rightarrow $ $Oy$ là tiệm cận đứng.
| $ \bullet $ Bảng biến thiên | $ \bullet $ Đồ thị |
|
|
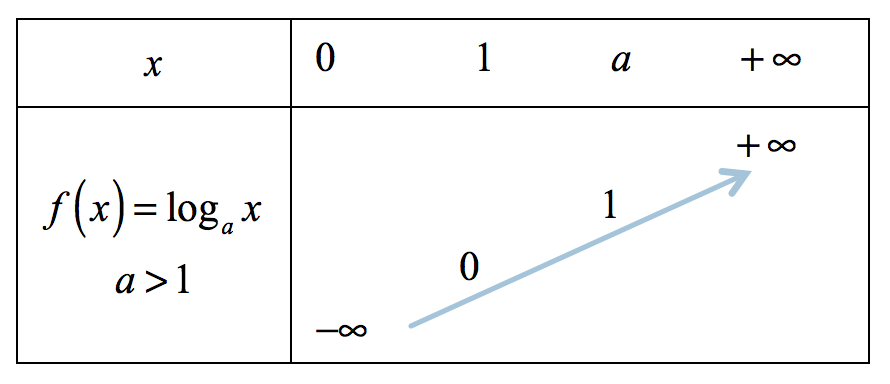
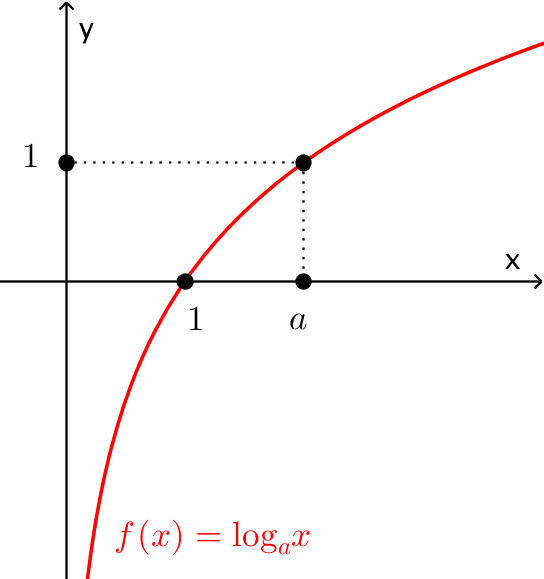
Trường hợp 2. $0<a<1$
$ \bullet $ Tập xác định $D = \left( {0; + \infty } \right).$
$ \bullet $ Sự biến thiên: Hàm số nghịch biến trên khoảng $D = \left( {0; + \infty } \right).$
$ \bullet $ Giới hạn $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } {\log _a}x = - \infty .$
$\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} {\log _2}x = + \infty \Rightarrow $ $Oy$ là tiệm cận đứng.
$ \bullet $ Sự biến thiên: Hàm số nghịch biến trên khoảng $D = \left( {0; + \infty } \right).$
$ \bullet $ Giới hạn $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } {\log _a}x = - \infty .$
$\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} {\log _2}x = + \infty \Rightarrow $ $Oy$ là tiệm cận đứng.
| $ \bullet $ Bảng biến thiên | $ \bullet $ Đồ thị |
|
|
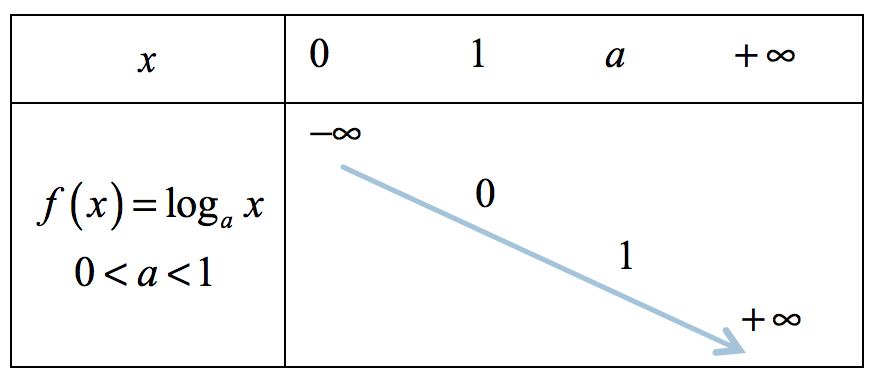
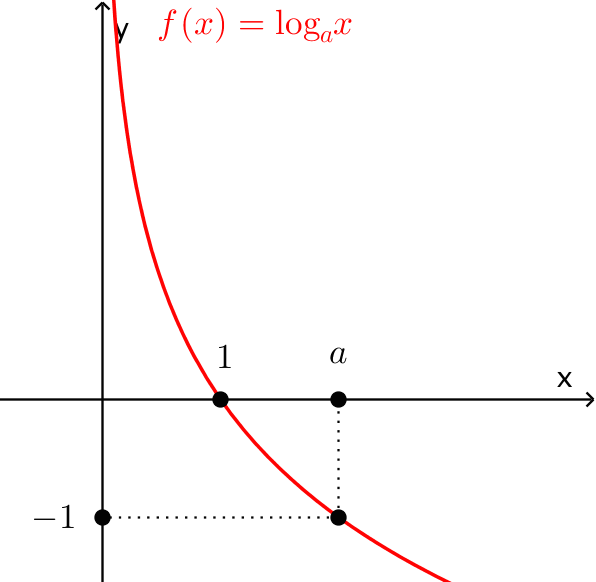
Ví dụ 2. Khảo sát và vẽ đồ thị hàm số $f\left( x \right) = {\log _2}x$.
$ \bullet $ Tập xác định $D = \left( {0; + \infty } \right).$
$ \bullet $ Sự biến thiên: Vì cơ số $ a=2>1$ nên hàm số đồng biến trên khoảng $D = \left( {0; + \infty } \right).$
$ \bullet $ Hàm số không có cực trị.
$ \bullet $ Sự biến thiên: Vì cơ số $ a=2>1$ nên hàm số đồng biến trên khoảng $D = \left( {0; + \infty } \right).$
$ \bullet $ Hàm số không có cực trị.
| $ \bullet $ Bảng biến thiên | $ \bullet $ Đồ thị |
|
|
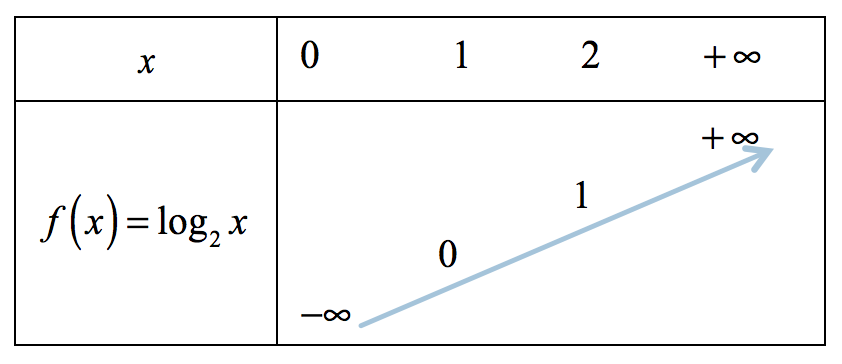
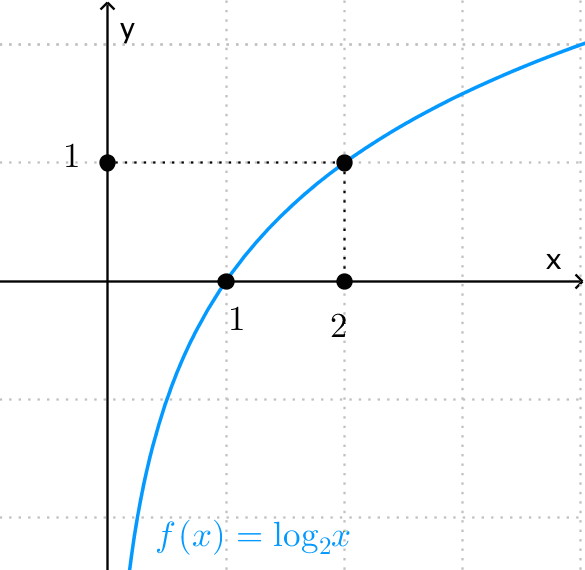
Bài tập
(nhiều bài tập hơn khi đăng ký học tại Trung tâm Cùng học toán)
Tác giả bài viết: Cùng Học Toán
Góp ý hoặc một bài toán của Quý học viên hoặc Quý Phụ Huynh