Tỷ mỷ làm toán. Độc lập suy nghĩ.

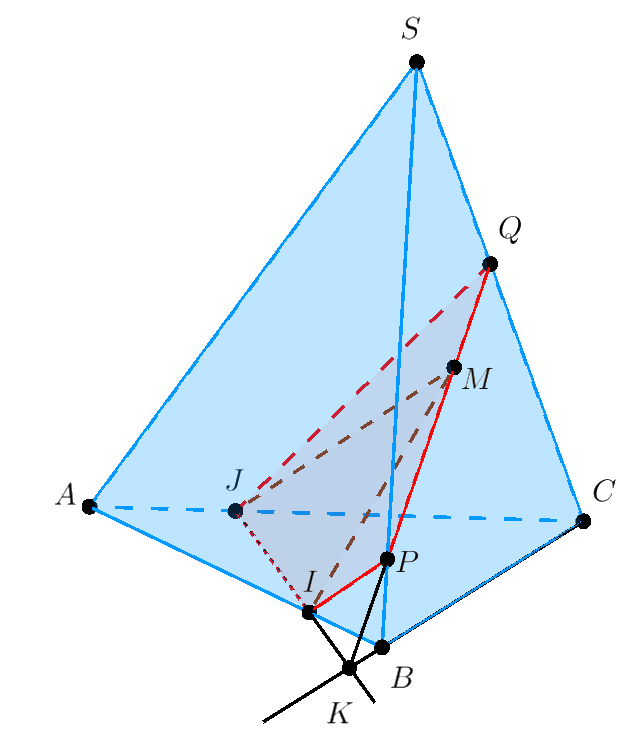
Giải. Ta lần lượt xác định giao tuyến $\hbox{(nếu có)}$ của mặt phẳng $\left( {MIJ} \right)$ với tất cả các mặt của hình chóp $S.ABC.$

$\bullet$ Xác định giao tuyến của $\left( {MIJ} \right)$ và $\left( {ABC} \right)$. $$\left( {MIJ} \right) \cap \left( {ABC} \right) = IJ.$$ $\bullet$ Xác định giao tuyến của $\left( {MIJ} \right)$ và $\left( {SBC} \right)$.
Trong mặt phẳng $\left( {ABC} \right)$ gọi $K = BC \cap IJ.$ Khi đó $K$ là điểm chung của $\left( {SBC} \right)$ và $\left( {ABC} \right)$. Suy ra $$\left( {MIJ} \right) \cap \left( {SBC} \right) = KM.$$ Trong mặt phẳng $\left( {SBC} \right)$ gọi $P$, $Q$ lần lượt là giao điểm của của $KM$ và $SB$, $SC$. Suy ra $PQ$ là đoạn giao tuyến của $\left( {MIJ} \right)$ và $\left( {SBC} \right)$.
Từ đây ta có

$\bullet$ Đoạn giao tuyến của $\left( {MIJ} \right)$ và $\left( {SAB} \right)$ là $IP$.

$\bullet$ Đoạn giao tuyến của $\left( {MIJ} \right)$ và $\left( {SAC} \right)$ là $JQ$.

Các đoạn giao tuyến trên tạo thành tứ giác $PQJI$. Đây cũng chính là thiết diện của hình chóp $S.ABC$ bị cắt bởi mặt phẳng $\left( {MIJ} \right)$.
 

---