Tỷ mỷ làm toán. Độc lập suy nghĩ.

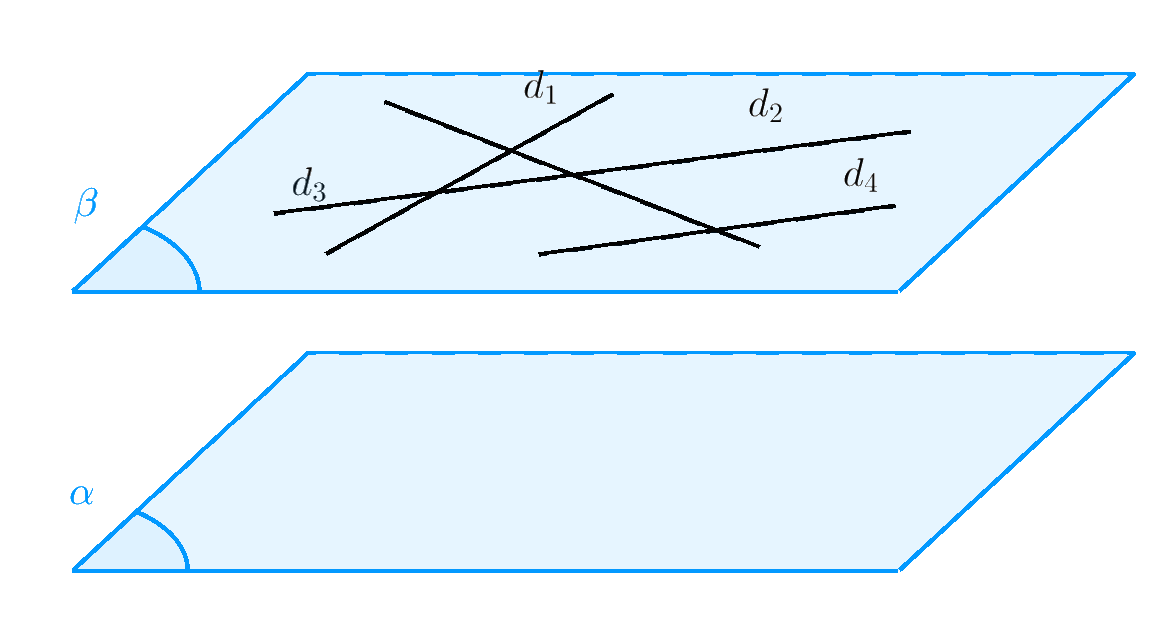
Mệnh đề. Nếu $(\alpha)$ song song với $(\beta)$ thì $(\alpha)$ song song với mọi đường thẳng nằm trong $(\beta)$. $$\left. \begin{array}{l}
\left( \beta  \right)//\left( \alpha  \right)\\
{d_1},{d_2},{d_3},{d_4},... \subset \left( \beta  \right){\rm{  }}
\end{array} \right\} \Rightarrow \left( \alpha  \right)//{d_1},{d_2},{d_3},{d_4},...$$




 

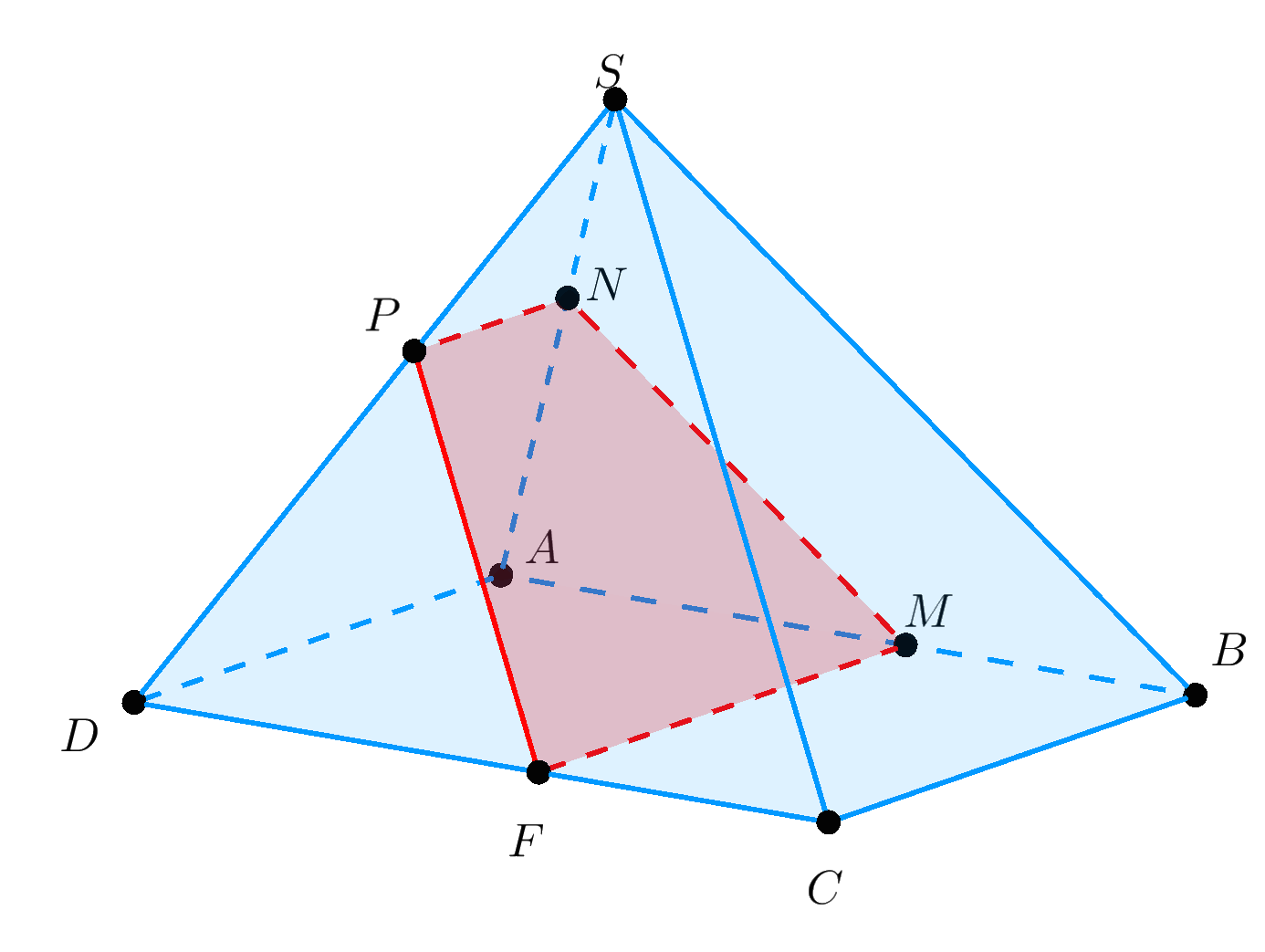
Ví dụ. Cho hình chóp $S.ABCD$ có đáy $ABCD$  là hình bình hành. Gọi $M$  là một điểm bất kỳ trên $AB.$  
Giả sử $\left( \alpha  \right)$  là mặt phẳng qua $M$  và song song với $\left( {SBC} \right).$  Tìm thiết diện của $S.ABCD$  cắt bởi $\left( \alpha  \right).$  
           Giải. Vì $\left( \alpha  \right)$  song song với $\left( {SBC} \right)$  nên $\left( \alpha  \right)//SB,SC,BC.$  
           
            Vì $\left( \alpha  \right)//SB \subset \left( {SAB} \right)$  nên   $\left( \alpha  \right) \cap \left( {SAB} \right) = MN//SB,\,\,N \in SA.$  
            Tương tự ta có $$\begin{array}{l}
\left( \alpha  \right) \cap \left( {ABCD} \right) = MF//BC,\,\,F \in DC.\\
\left( \alpha  \right) \cap \left( {SCD} \right) = FP//SC,\,\,P \in SD.
\end{array}$$Vậy $MNPF$  là thiết diện cần tìm.

 

---