Tích vô hướng của hai vector. Ứng dụng.
Tích vô hướng của hai vector. Ứng dụng tích có hướng của hai vector tính độ lớn của vector. Ứng dụng tích vô hướng của hai vector chứng minh hai đường thẳng vuông góc.
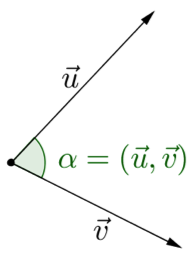
Định nghĩa. Tích vô hướng của hai vector $\vec u$ và $\vec v$, ký hiệu $\vec u \cdot \vec v,$ là một số thực được định nghĩa như sau $$\vec u \cdot \vec v = \left| {\vec u} \right| \cdot \left| {\vec v} \right| \cdot \cos \alpha ,$$ trong đó $\alpha = \left( {\vec u,\vec v} \right)$ là góc hợp bởi hai vector $\vec u$ và $\vec v$.
Ví dụ 1. Giả sử $\left| {\vec u} \right| = a,{\text{ }}\left| {\vec v} \right| = b,{\text{ }}\left( {\vec u,\vec v} \right) = {60^o}$ thì $$\vec u \cdot \vec v = \left| {\vec u} \right| \cdot \left| {\vec v} \right| \cdot \cos \left( {\vec u,\vec v} \right) = a \cdot b \cdot \cos {60^o} = \frac{{ab}}{2}.$$
Ứng dụng tích vô hướng để tính độ dài vector. Cho $\vec a$ là một vector bất kì trong không gian. Vì $\left( {\vec a,\vec a} \right) = \vec 0$ nên $\vec a \cdot \vec a = \left| {\vec a} \right| \cdot \left| {\vec a} \right|\cos \left( {\vec a,\vec a} \right) = {\left| {\vec a} \right|^2}\cos {0^o} = {\left| {\vec a} \right|^2}.$ Từ đây suy ra $$\left| {\vec a} \right| = \sqrt {{{\vec a}^2}} .$$
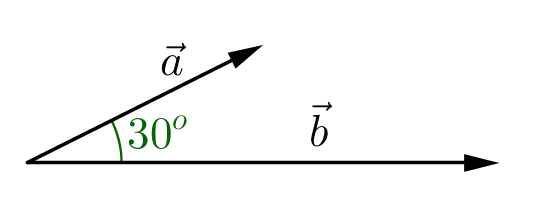
Ví dụ 2. Trong không gian cho hai vector $\vec a$ và $\vec b$ hợp nhau một góc $\left| {\vec a} \right| = 3,{\text{ }}\left| {\vec b} \right| = 5.$ Bây giờ ta tính độ lớn của vector tổng $\left| {\vec a + \vec b} \right|$. Ta có$${\left( {\vec a + \vec b} \right)^2} = {{\vec a}^2} + 2 \cdot \vec a \cdot \vec b + {{\vec b}^2} = {\left| {\vec a} \right|^2} + 2\left| {\vec a} \right|\left| {\vec b} \right|\cos \left( {\vec a,\vec b} \right) + {\left| {\vec b} \right|^2} = 9 + 2 \cdot 3 \cdot 5 \cdot \cos {30^o} + 25 = 34 + 15\sqrt 3 .$$
Ứng dụng tích vô hướng để tính chứng minh hai đường thẳng vuông góc. Trong không gian, cho hai hai đường thẳng $a$ và $b$ lần lượt có vector chỉ phương là $\vec u$ và $\vec v$, từ mối liên hệ giữa góc hợp bởi hai đường thẳng và góc hợp bởi hai vector chỉ phương ta có $a \bot b \Leftrightarrow \vec u \bot \vec v \Leftrightarrow \left( {\vec u,\vec v} \right) = {90^o} \Rightarrow \vec u \cdot \vec v = \left| {\vec u} \right| \cdot \left| {\vec v} \right|\cos {90^o} = 0.$ Tóm lại $$a \bot b \Leftrightarrow \vec u \cdot \vec v = 0.$$ Ứng dụng này sẽ bàn kĩ hơn ở bài Hai đường thẳng vuông góc.
Bài tập
Tác giả bài viết: Cùng Học Toán




Góp ý hoặc một bài toán của Quý học viên hoặc Quý Phụ Huynh